Hi everyone! I am glad to announce that Zalando CodeSprint on HackerRank is scheduled on June 4, 2016, 12:00 PM CEST. Contest duration is 24 hours, but don't be scared by that. There will be 8 problems to solve.
Sign up here: https://www.hackerrank.com/zalando-codesprint
The prizes are:
- Rank 1: Pebble Watch, 200 Euro gift voucher of your choice, Hackathon Hoodie
- Rank 2-5: 200 Euro gift voucher of your choice, Hackathon Hoodie
- Rank 6-20: Hackathon Hoodie









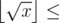 (long) Math.sqrt(x)
(long) Math.sqrt(x) 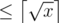 ?
?