I'll just leave this here:
#include <bits/stdc++.h>
using namespace std;
struct _in {
template<class T> operator T() {
T x;
cin >> x;
return x;
}
} in;
int main() {
vector a(in, 0.0);
for (auto& x : a) x = in;
string s = in;
cout << s << ' ' << a[2] << '\n';
}
Try with input
5
0.1 0.2 0.3 0.4 0.5
hello
Have a nice day









 such sequences, in time
such sequences, in time  — perhaps there is a better algorithm but this was good enough for my problem. The final complexity is
— perhaps there is a better algorithm but this was good enough for my problem. The final complexity is 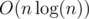 .
.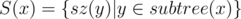 for all
for all  . I used class templates to save some memory — this is another interesting idea and a topic on its own.
. I used class templates to save some memory — this is another interesting idea and a topic on its own.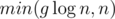 new nodes and take
new nodes and take 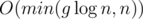 time. To understand this, think of what happens when one of the sets has 1, 2, or 3 elements.
time. To understand this, think of what happens when one of the sets has 1, 2, or 3 elements. . You now have access to all the sets, for each node.
. You now have access to all the sets, for each node.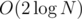 of them. We may also visit some others but we will exit immediately as their total is
of them. We may also visit some others but we will exit immediately as their total is  , and also
, and also  . Also, I wanted to try a new approach and see if it's efficient enough. And as it turns out, it is! :)
. Also, I wanted to try a new approach and see if it's efficient enough. And as it turns out, it is! :)
