We invite you to participate in CodeChef’s March Lunchtime, this Saturday, 27th March.
Time: 7:30 PM — 10:00 PM IST. Please note the change in timings. This contest will end at 10 PM instead of the usual 10:30 PM.
The March Lunchtime is going to have Gameskraft, Quadeye Securities, Dialpad, and BetterPlace as the official contest recruiters! Gameskraft is hiring for Javascript and Frontend Developers. Quadeye is on the lookout for brilliant Full Stack Developers in CodeChef’s community. Dialpad is looking to attract top talent from CodeChef for the role of Software Engineer. BetterPlace is looking to hire competent coders from the community for SDE 1 and SDE 2 roles.
Also, if you have some original and engaging problem ideas, and you’re interested in them being used in CodeChef's contests, you can share them here.
Joining us on the problem setting panel are:
Setters: Le Duc Minh, nbmnb, nhdtxdy, Quân Anh
Testers: Shubham TheOneYouWant Anand Jain, Aryan aryanc403 Choudhary, Trùng Mễ, Tran thenymphsofdelphi Xuan Bach, Quang xuanquang1999 Nguyen
Statement Verifier: Jakub Xellos Safin
Editorialist: Nishank IceKnight1093 Suresh
Admin: Jatin jtnydv25 Yadav
Video Editorialists: Chirayu Chirayu Jain, Prachi agarwal19 Agarwal, Darshan darshancool25 Lokhande, Yashodhan ay21 Agnihotri, Bharat Singla, Shivam Bohra, Radoslav radoslav11 Dimitrov, Aryan Agarwala, Meet myth_gemphir Singh Gambhir
Mandarin Translator: Gedi gediiiiiii Zheng
Vietnamese Translator: Team VNOI
Russian Translator: Fedor Mediocrity Korobeinikov
Bengali Translator: Mohammad solaimanope Solaiman
Prizes:
We are doubling the happiness this Lunchtime.
Since it's our birthday month, the Chef is in a generous mood. We shall be giving away prizes to double the number of winners than usual. For example: Instead of Top 10, Top 20 will get the winner laddus. This is applicable across all category winners.
There are also special prizes for women:
- Div 1: top 10 females (300 laddus)
- Div 2: top 6 females (150 laddus)
- Div 3: top 6 females (150 laddus)
The winners can claim cool CodeChef goodies using these laddus. Know more here.
The video editorials of the problems will be available on our YouTube channel as soon as the contest ends. Subscribe to get notifications about our new editorials.
Good Luck!
Hope to see you participating!!
Happy Programming!!








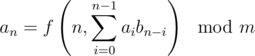
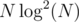 .
. 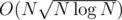 which works in almost the same time as
which works in almost the same time as 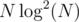 solution because of a very low constant. Here goes:
solution because of a very low constant. Here goes: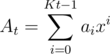 .
. times using FFT in time
times using FFT in time 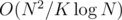 .
.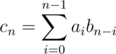

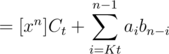 .
. , which is minimized taking
, which is minimized taking 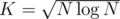 , and overall complexity is
, and overall complexity is 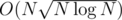 .
.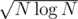 for better results, because of a huge constant difference in the two parts. (Computing
for better results, because of a huge constant difference in the two parts. (Computing 
