450A - Jzzhu and Children
You can simply simulate it or find the last maximum ceil(ai / m).
450B - Jzzhu and Sequences
We can easily find that every 6 numbers are the same. It's like {x, y, y - x, - x, - y, x - y, x, y, y - x, ...}.
449A - Jzzhu and Chocolate / 450C - Jzzhu and Chocolate
We assume that n ≤ m (if n > m, we can simply swap n and m).
If we finally cut the chocolate into x rows and y columns (1 ≤ x ≤ n, 1 ≤ y ≤ m, x + y = k + 2), we should maximize the narrowest row and maximize the narrowest column, so the answer will be floor(n / x) * floor(m / y).
There are two algorithms to find the optimal (x, y).
Notice that if x * y is smaller, the answer usually will be better. Then we can find that if k < n, the optimal (x, y) can only be {x = 1, y = k + 1} or {x = k + 1, y = 1}. If n ≤ k < m, the optimal (x, y) can only be {x = 1, y = k + 1}. If m ≤ k ≤ n + m - 2, the optimal (x, y) can only be {x = k + 2 - m, y = m}, because let t = m - n, n / (k + 2 - m) ≥ (n + t) / (k + 2 - m + t) ≥ 1.
floor(n / x) has at most
 values, so we can enum it and choose the maximum x for each value.
values, so we can enum it and choose the maximum x for each value.
449B - Jzzhu and Cities / 450D - Jzzhu and Cities
We consider a train route (1, v) as an undirected deletable edge (1, v).
Let dist(u) be the shortest path between 1 and u. We add all of the edges (u, v) weighted w where dist(u) + w = dist(v) into a new directed graph.
A deletable edge (1, v) can be deleted only if it isn't in the new graph or the in-degree of v in the new graph is more than 1, because the connectivity of the new graph won't be changed after deleting these edges. Notice that you should subtract one from the in-degree of v after you delete an edge (1, v).
449C - Jzzhu and Apples / 450E - Jzzhu and Apples
Firstly, we should notice that 1 and the primes larger than N / 2 can not be matched anyway, so we ignore these numbers.
Let's consider each prime P where 2 < P ≤ N / 2. For each prime P, we find all of the numbers which are unmatched and have a divisor P. Let M be the count of those numbers we found. If M is even, then we can match those numbers perfectly. Otherwise, we throw the number 2P and the remaining numbers can be matched perfectly.
Finally, only even numbers may be unmatched and we can match them in any way.
449D - Jzzhu and Numbers
Firstly, we can use inclusion-exclusion principle in this problem. Let f(x) be the count of number i where Ai&x = x. Let g(x) be the number of 1 in the binary respresentation of x. Then the answer equals to 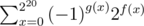 .
.
Now the task is to calculate f(x) for every integer x between 0 and 220. Let fk(x) be the count of number i where Y0&X0 = X0 and X1 = Y1 (they are defined below).
We divide x and Ai into two parts, the first k binary bits and the other 20 - k binary bits. Let X0 be the first part of x and X1 be the second part of x. Let Y0 be the first part of Ai and Y1 be the second part of Ai.
We can calculate fk(x) in O(1):
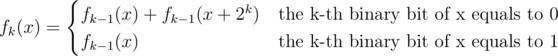
The problem can be solved in O(n * 2n) now (n = 20 in this problem).
449E - Jzzhu and Squares
Consider there is only one query.

Let me descripe the picture above.
A grid-square can be exactly contained by a bigger square which coincide with grid lines. Let L be the length of a side of the bigger square. Let i be the minimum distance between a vertice of the grid-square and a vertice of the bigger square. Let f(L, i) be the number of cells which are fully contained by the grid-square.
We can divide a grid-square into four right triangles and a center square. For each right triangle, the number of cells which are crossed by an edge of the triangle is L - gcd(i, L). Then, the number of cells which are fully contained by the triangle is [i(L - i) - L + gcd(i, L)] / 2.
f(L, i) = (L - 2i)2 + 2[i(L - i) - L + gcd(i, L)] = L2 - 2iL + 2i2 - 2L + 2gcd(i, L)
Firstly, we enum L from 1 to min(N, M). Then the task is to calculate 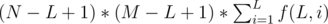 .
. 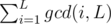 can be calculated by the following steps:
can be calculated by the following steps:
Enum all of the divisor k of L and the task is to calculate the count of i where gcd(i, L) = k.
The count of i where gcd(i, L) = k equals to φ(L / k).
Finally,  .
.
If there are multiple queries, we can calculate the prefix sum of 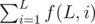 ,
, 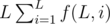 and
and 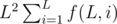 , then we can answer each query in O(1).
, then we can answer each query in O(1).










