615A - Bulbs (Author: TheWishmaster)
Let's make a counter of number of buttons that switch every lamp off. If there is a lamp with zero counter, output NO, otherwise YES.
code: 15260902
615B - Longtail Hedgehog (Author: TheWishmaster)
Way of solving — dynamic programming. We are given a graph of n vertices and m edges. We will calculate dp[i] — a maximum length of tail that is ending in i-th vertex. We can simply update dp by checking all the edges from i-th vertex(which are leading to vertices with bigger number), and trying to update them. When we have this dp, we can check the answer easily.
code: 15260851
615C - Running Track (Author: maxkvant)
The idea is that if can make a substring t[i, j] using k coatings, then we can also make a substring t[i + 1, j] using k coatings. So we should use the longest substring each time.
Let n = |s|, m = |t|. On each stage we will search for the longest substring in s and s_reversed to update the answer. We can do it in several ways:
- Calculate lcp[i][j] — longest common prefix t[i, m] and s[j, n], lcprev[i][j] — longest common prefix t[i, m] and s[j, 1]. Find longest means find max(max(lcp[i][1], lcp[i][2], ..., lcp[i][n]), max(lcprev[i][1], lcprev[i][2], ..., lcprev[i][n])).
calculation lcp:
for (int i = m; i >= 1; i--)
for (int j = n; j >= 1; j--)
if (t[i] == s[j])
lcp[i][j] = lcp[i + 1][j + 1] + 1;
code: 15277213
Let's check iterative t[i, i ] exists in s as a substring, t[i, i + 1] t[i, i + 2] .... We will make an array endPos, where endPos[j] is true when t[i, i + cur_len - 1] = s[j - cur_len + 1, j] (t[1, i — 1] greedy already got). We will update this array, adding symbols t[i], t[i + 1], t[i + 2] and so on. We will make one more array — for s_reversed. (more details in code)
Overall time complexity will be 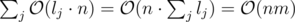
code: 15260867
trie solution: 15260870
bonus
Can you solve with 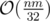 complexity?
complexity? 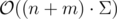 ?
? 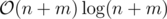 ?
?
Σ — alphabet size.
615D - Multipliers (Author: maxkvant)
Let d(x) be a number of divisors of x, and f(x) be the product of divisors. Let x = p1α1p2α2... pnαn, then d(x) = (α1 + 1)·(α2 + 1)... (αn + 1)
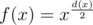 . There is
. There is 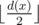 pairs of divisors of type
pairs of divisors of type 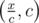 ,
, 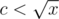 , and if x is a perfect square we have one more divisor :
, and if x is a perfect square we have one more divisor : 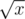 .
.
for a prime m and a ≠ 0 the statement 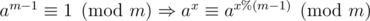 (little Fermat theorem)
(little Fermat theorem)
We can see that 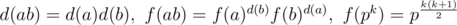 , if a and b are co prime.
, if a and b are co prime.
Now we can count the answer:
d = 1;
ans = 1;
for (int i = 0; i < l; i++) {
fp = binPow(p[i], (cnt[i] + 1) * cnt[i] / 2);
ans = binPow(ans, (cnt[i] + 1)) * binPow(fp, d) % MOD;
d = d * (cnt[i] + 1) % (MOD - 1);
}
code: 15260890
bonus
Another problem.
Given secquence (p1, k1), (p2, k2), ..., (pn, kn)
(pi — distinct primes) and q queries (l, r) to calculate f(plkl·pl + 1kl + 1... prkr)%MOD.
Can you solve with 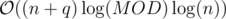 complexity?
complexity?
Suppose r - l + 1 = M = const in all queries. Can you solve with 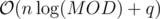 complexity?
complexity?
615E - Hexagons (Author: TheWishmaster)
Let's see how the coordinates are changing while we move from current cell to one of the 6 adjacent cells — let's call this 6 typed of moves. If we know the number of moves of each type on our way, then we know the coordinates of the end of the way. We will divide the way into rings.
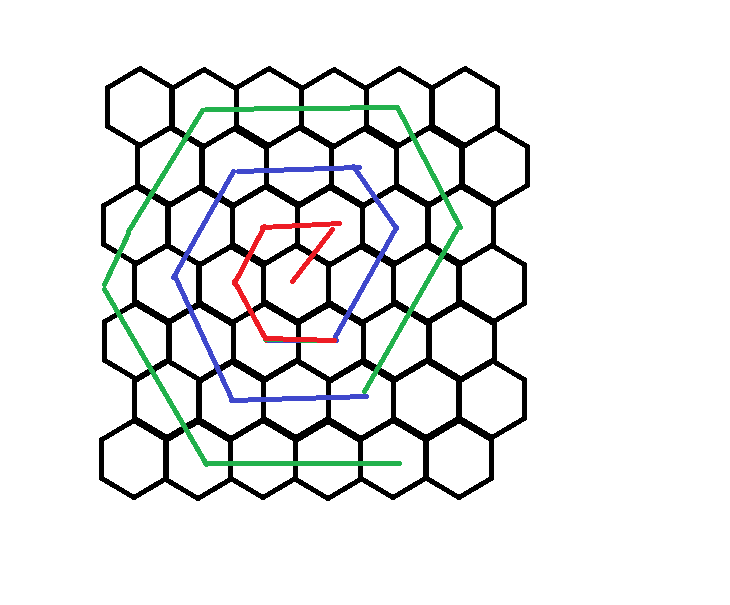
Let's count the number of moves of each type for the first ring. Next ring will have one more move of each type. Length of each ring = length of previous + 6. It is an arithmetic progression. Using well-known formulas and binary search we calculate the number of the last ring and overall length of previous rings. Now we have to brute-force 6 types of the last move and calculate the answer.
code: 15260879









