Contest Link: http://acm.hust.edu.cn/vjudge/contest/view.action?cid=103450#overview
This editorial was written by atrista. I am just posting in CF.
Problem A:
Problem summary: Given a n * m grid G, we have to go from top-left corner to bottom right corner where the cost of stepping to cell (i, j) is denoted by G[i][j] which is always positive.
Solution: We can use straight-forward Dijkstra for this problem. Simple Dijkstra with starting node (0, 0) with initial cost of G[0][0] and ended on (n - 1, m - 1) will do the job.
One of the participant, moudud99's code: http://paste.ubuntu.com/14416006/
Problem B:
Problem Summary: Given a list of walls and doors, we have to find shortest path from cell(0, 0) to a cell(x, y) where cost is corresponded to number of doors we have to pass through out the path.
Solution: The main issue in the problem is certainly graph construction. We are given a list of walls either horizontal or vertical. We can represent the graph like this
int grid[N][N][4]; where grid[i][j][l] = 0 / 1 / 2. if 0, nth side of cell (i, j) doesn’t have a wall nor its a door, if 1, then it has wall, if 2 is a wall. We can assume if l=0 then the direction is up, if l=1 then the direction is left, if l=2 then the direction is right, if l=3 then direction is down. When we get a vertical update, we update both grid[i][j][1] and grid[i][j - 1][2]. For a horizontal update, we update both grid[i][j][3] and grid[i - 1][j][0].
After that we can use a variant of bfs where we fill the wall and door separated and consider them as a single node. Or we can just use a Dijkstra and do this simple we do in simple graph.
A code that follows the bfs idea: http://paste.ubuntu.com/14417087/
One of the participant, Anindya_Buet’s code: http://paste.ubuntu.com/14417071/
Problem C:
Problem Summary: Given a weighted graph G, where weight can be negative, we have to find out if there is a negative cycle in the graph.
Solution: We can use Bellman Ford algorithm for this task. We know, for a graph of n nodes, if there is no negative cycle the length of the path can have almost n nodes which are added by n - 1 iterations. If after another extra iteration we can reduce the cost for any node then, there exists a negative cycle.
A very simple code that follows the idea from IOI_ruhanhabib39’s who solved the problem: http://paste.ubuntu.com/14417177/
Problem D:
This is one of the most elegant problems of the contest.
Problem Summary: Given a graph and a sequence of node, we have to simulate the effect of removing nodes and corresponding edges in the graph and have to output the sum of cost of all pair shortest paths.
Solution: We need a good understanding of Floyd Warshall algorithm for this problem. Floyd Warshal relaxes a path between all pair of nodes using an intermediate node. The order of relaxation is dependent on the sequence by which the nodes are removed. But as simulating the removing is tough, so we calculate the result from backward and starting with an empty graph we simulate adding nodes in reverse.
Code that follows the idea: http://paste.ubuntu.com/14417195/
Code from participant Anindya_Buet: http://paste.ubuntu.com/14417349/
Problem E:
This used to be my most favourite problem from the contest set.
Solution: Instead of just calculating the path with maximum probability of a packet successfully getting through, we can simple calculate the path with minimum probability of a packet not getting through. After that, this is simple expectation calculation.
Code that follows this idea: http://paste.ubuntu.com/14417450/
Code from participant Anindya_Buet: http://paste.ubuntu.com/14417472/
moinul.shaon's comment:
Use dijkstra to calculate minimum probability p. So expected time for unit data E is E = p * 2k + (1 - p) * (2k + E). Solve it and you will get E = 2k / p for unit data. So for S data answer is 2kS / p
Problem F:
Simple Miser Nim game.
Solution: Miser Nim is a Nim game unless all pile size is 1. If all pile sizes are 1 then this is simply a odd even game.
Code from participant IOI_tasmeemreza : http://paste.ubuntu.com/14417512/
Problem G:
Solution: This is exactly a Nim game where the pile size in just the distance between gray and white pieces.
Code: http://paste.ubuntu.com/14417564/
Problem H:
Solution: This is a problem of finding Grundy number. A great analysis of this problem can be found in topcoder: https://www.topcoder.com/community/data-science/data-science-tutorials/algorithm-games/ Notice the Composite games – Grundy numbers section.
We simply calculate the grundy number for n*n grid and simply xor the grundy numbers for cells where the hyper knights are.
Instead of just calculating Grundy for every case, we can precalc it.
Code from participant nmunim : http://paste.ubuntu.com/14417606/
Problem I:
Solution: This is simply game theory themed DP problem. Let dp[i] be 0/1. dp[i] = 1 if there at least 1 winning state from this for the player no matter who is playing, with i stones.
So, dp[i] = 1 if any of dp[i - a[j]] = 0 where a[j] denotes a legal move. So, if dp[n] = 1 then Stan wins else Ollie wins.
Code from participant moudud99: http://paste.ubuntu.com/14417642/
Problem J:
Solution: In this type of game problem, then we are dividing the pile into two or more piles then the grundy numbers that are affecting the grundy of initial pile is xor of the child piles.
So, for pile size x, grundy[x] is the smallest number that isn’t in the set consisted of grundy[i] xor grundy[x - i] where i < = x / 2 and not equals x - i.
Then we simply xor the grundy numbers corresponded to the pile size.
Code implementing the following idea from zawadabdullah : http://paste.ubuntu.com/14417707/
Thank you.









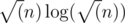 ) and treap is O( log(n)*log(n) ) . Both of my method took ~3.3s and ~4.5s respectively . I want to know if there is any faster method as there seems to be ~1s solution on the statistics.
) and treap is O( log(n)*log(n) ) . Both of my method took ~3.3s and ~4.5s respectively . I want to know if there is any faster method as there seems to be ~1s solution on the statistics.
