Can somebody describe their solution to http://codeforces.com/gym/100519/problem/I ? Somehow I can't shake the feeling that it's enough to always multiply with 2, but I cannot substantiate my intuition to turn this into an algorithm.
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3650 |
| 2 | Benq | 3582 |
| 3 | Geothermal | 3570 |
| 3 | orzdevinwang | 3570 |
| 5 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3532 |
| 8 | Radewoosh | 3522 |
| 9 | Um_nik | 3483 |
| 10 | jiangly | 3468 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 163 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
Earlier this day I came across a delightfully interesting question about an algorithm problem: http://stackoverflow.com/questions/23490944/recreate-the-sequence
Basically it asks:
Alice has written N consecutive, positive integers on a blackboard. E.g. "99, 100, 101, 102". Bob has erased all digits, but one, from each number, so the sequence now reads e.g. "9, 0, 0, 1".
So for every number in the sequence, Bob leaves over exactly one digit, and the position of that digit can vary between the numbers.
You are given the list of remaining digits and you should reconstruct the smallest starting value (in this case, 99) that could have resulted in the given sequence of digits.
OP claims there exists an  algorithm. I suggested an
algorithm. I suggested an 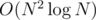 algorithm for a starter, but I'm convinced we can do better. Any ideas?
algorithm for a starter, but I'm convinced we can do better. Any ideas?
I wrote a post about how to tackle certain problems on numbers using dynamic programming techniques over at Stack Overflow. This includes tasks like
- "Find the sum of integers X with digit sum S, where X <= Y" (Y given)
- "Find the number of palindromic integers between L and R"
- "Enumerate all integers between L and R that only have digits 4 and 7"
- "Find the probability that an integer X uniformly chosen from the range [L,R] has at least 10 common digits with a given number S"
that can all be solved with a very similar idea. Just in case somebody's interested.
Good morning ;)
I'm currently improving my geometry code collection and searching for programming tasks involving numerical integration to test my code.
So far, I found the following:
- SGU 217 "Two Cylinders"
- ZOJ 2675 "Little Mammoth"
- UVa 12528 "Environment Protection" (thanks Hernan and mohammadrdeh)
- UVa 1280 "Curvy Little Bottles" (thanks Hernan)
- Timus 1562 "GM-pineapple" (thanks kolya37)
- SPOJ "CIRU" (thanks TobiichiOrigami)
I have to add that most of these can be solved explicitly as well :)
Do you know any similar tasks?
I'm using the following code (which I have not written myself!) which is a simple implementation of the adaptive Simpson's rule and which has served me quite well so far:
double simps(double a, double b) {
return (f(a) + 4*f((a+b)/2) + f(b))*(b-a)/6;
}
double integrate(double a, double b){
double m = (a+b)/2;
double l = simps(a,m), r = simps(m,b), tot=simps(a,b);
if (fabs(l+r-tot) < eps) return tot;
return integrate(a,m)+integrate(m,b);
}
| Name |
|---|










