I have found an interesting problem like this: there are $$$n$$$ kind of cakes and for $$$1 \le i \le n$$$, there are $$$a_i$$$ cakes of the $$$i-$$$th kind. We need to take out as much as $$$k-$$$ tuples of distinct cakes. So with the given value of $$$k \ge 1$$$ and array $$$a_1,a_2,...,a_n$$$, what is the maximum number of tuples can we get?
For example: we have $$$4$$$ kinds of cake as $$$(A,B,C,D)$$$ with amounts: $$$a[4] = (20,30,40,50)$$$ and $$$k=3$$$. We can get at most $$$45$$$ tuples as: $$$5$$$ tuples $$$(A,B,C)$$$ and $$$15$$$ tuples $$$(A,C,D)$$$ and $$$25$$$ tuples $$$(B,C,D)$$$.
I came up with this idea to solve as follow:
By this idea, for the test case as: $$$a[5] = (1,2,3,1000,1000)$$$ and $$$k=4$$$, I got the answer is $$$3$$$ after some iterations. And by checking with some other tricky test cases, I'm pretty sure this idea is true.
I have two questions: Is this problem new? And how to find a proof for this approach? Thanks for your help.








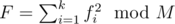 in which
in which 

