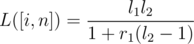First, I really need to apologize for the round. There was a serious problem in D that was even covered in the sample test, that the main solution did not handle correctly. I should have been much more careful with this problem and looked for these kind of cases. Unfortunately, it was a big enough issue that caused the round to be unrated. I know this upset a lot of people, but it's tricky to find a solution to this kind of problem after the problem has happened.
I still hope the problems were good quality. If you learned something new from the round, or from this editorial, then the round was worth it. I would advise to solve the problems you couldn't solve during the contest, so you can take away something from the round.
If you want any further clarification on a problem, please ask in comments!
821A — Okabe and Future Gadget Laboratory
We can simulate exactly what's described in the statement: loop over all cells not equal to 1 and check if it doesn't break the city property. To check if a cell breaks the property, just loop over an element in the same row, and an element in the same column, and see if they can add to give the cell's number. The complexity is O(n4).
Sidenote: The definition of lab here was actually inspired from a USAMTS problem in 2016.
The critical observation to make is that the optimal rectangle should always have a lower-left vertex at the origin. This is due to the fact that the line has positive y-intercept and negative slope: any rectangle which doesn't have a vertex at the origin could easily be extended to have a vertex at the origin and even more bananas.
Then, we just need to try every x-coordinate for the upper-right corner of the box and pick the maximum y-coordinate without going over the line. We can compute the sum of any rectangle in O(1) using arithmetic series sums, so this becomes O(bm) because the x-intercept can be up to bm. You can make it faster by trying every y-coordinate; this makes the complexity O(b), but this was unnecessary to solve the problem.
 Can you solve the problem with better complexity?
Can you solve the problem with better complexity?
It looks like Daru should only reorder the boxes when he has to (i.e. he gets a remove operation on a number which isn't at the top of the stack). The proof is simple: reordering when Daru has more boxes is always not worse than reordering when he has less boxes, because Daru can sort more boxes into the optimal arrangement. Therefore, our greedy algorithm is as follows: simulate all the steps until we need to reorder, and then we resort the stack in ascending order from top to bottom.
This has complexity O(n2 log n). However, we can speed this up if we note that whenever we reorder boxes, any box currently on the stack can be put in an optimal position and we can pretty much forget about it. So whenever we reorder, we can just clear the stack as well and continue. This gives us O(n) complexity because every element is added and removed exactly once.
First, let's make this problem into one on a graph. The important piece of information is the row and column we're on, so we'll create a node like this for every lit cell in the grid. Edges in the graph are 0 between 2 nodes if we can reach the other immediately, or 1 if we can light a row/column to get to it. Now it's a shortest path problem: we need to start from a given node, and with minimum distance, reach another node.
Only problem is, number of edges can be large, causing the algorithm to time out. There are a lot of options here to reduce number of transitions. The most elegant one I found is Benq's solution, which I'll describe here. From a given cell, you can visit any adjacent lit cells. In addition, you can visit any lit cell with difference in rows at most 2, and any lit cell with difference in columns at most 2. So from the cell (r,c), you can just loop over all those cells.
The only tricky part is asking whether the current lit row/column should be a part of our BFS state. Since we fill the entire row/col and can then visit anything on that row/col, it doesn't matter where we came from. This means that you can temporarily light each row/column at most once during the entire BFS search.
So complexity is O(n + m + k), with a log factor somewhere for map or priority queue. Interestingly enough, you can remove the priority queue log factor because the BFS is with weights 0 and 1 only, but it performs slower in practice.
You can see the code implementing this approach below.
Another approach to this problem was using "virtual nodes". Virtual nodes are an easy way to put transitions between related states while keeping number of edges low. In this problem, we can travel to any lit cell if its row differs by <=2, or its column differs by at most 2, but naively adding edges would cause O(k^2) edges.
Instead, for every row, lets make a virtual node. For every lit cell in this row, put an edge between the lit cell and this virtual node with cost 1. We can do something similar for every column.
Now, it's easy to see that the shortest path in this graph suffices. A minor detail is that we should divide the answer by 2 since every skipping of a row or column ends up costing 2 units of cost.
821E — Okabe and El Psy Kongroo
You can get a naive DP solution by computing f(x, y), the number of ways to reach the point (x, y). It's just f(x - 1, y + 1) + f(x - 1, y) + f(x - 1, y - 1), being careful about staying above x axis and under or on any segments.
To speed it up, note that the transitions are independent of x. This is screaming matrix multiplication! First, if you don't know the matrix exponentiation technique for speeding up DP, you should learn it from here.
Now, let's think of the matrix representation. Since the x dimension is the long one and the y dimension is small, lets store a vector of values dp where dpi is the number of ways to get to a y value of i at the current x value. This will be the initial vector for matrix multiplication.
Now, what about the transition matrix? Since our initial vector has length y and we need a matrix to multiply it with to map it to another vector with length y, we need a y by y matrix. Now, if you think about how matrix multiplication works, you come up with an idea like this: put a 1 in the entry (i,j) if from a y value of i we can reach a y value of j (i.e. |i - j| ≤ 1). Don't believe me, multiply some vector times a matrix of this form to see how and why the transition works.
You can then build this matrix quickly and then matrix exponentiate for under every segment and multiply by the initial vector, then make the result as the new initial vector for the next segment. You should make sure to remove values from the vector if the next segment is lower, or add values to the vector if the next segment is higher. This gives complexity O(nh3 log w) where h = 16 and w = k.








 moves, and same for
moves, and same for  , and the coefficient to
, and the coefficient to