| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 162 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
Recently I made up my first post and now I go on!
This year I tried streaming me playing hearthstone since I was playing not bad, also my contest perfomances slightly grew up so I decided to create a screencast!
Today was first time I could ran without any technical issues, so you can watch me competing in SRM 661.
Here's a link for my screencast(with random commentaries on russian :D). Also you can check my channel where I'm going to post other videos from Codeforces and Topcoder rounds.
I dont know how you like this but anyway I would be glad to see you comments and suggestions.
Hi, It's my first blogpost on codeforces.
I was preparing problems for today srm and now want to tell about hardest problem from problemset.
This is a short editorial for srm 660 div1hard problem.
You probably should not read it if you dont know the problem yet and want to train to solve hard problems by yourself :)
Here is a link for the statement.
First you can see that morphing operation is reversible(if you can transform array a to array b, then you can also transform b to a by the same operation). So if you imagine that arrays are vertices of some graph where two arrays is connected if it's possible to transform one from another, the minimal number of vertices needed so any can be reached is just a number of connected components in this graph.
Now I say that this problem about counting non-isomorphic directed graphs with outgoing degree 1 and ingoing at most k. You can see why :)
First lets consider that some array is a matrix of 0s and 1s. For each i, lets put 1 in cell(i, a[i]) in matrix. We've got a matrix with one 1 in each row and at most k 1s in each column. So there is a bijection between arrays and matrixes. It should to be noticed that morphing operation works on matrix as swap of two rows (x, y), and two columns (x, y).
Ok. We know that matrix of 0s and 1s could be used as presentation of directed unweighted graph. So not lets consider that array from this problem is directed graph, additional requarement is that outgoing degree of each vertes is 1 and ingoing is at most k. And finally morphing operation is just a swap of indexes of two vertexes.
Picture shows what happens with array {2,3,2,4} and corresponding matrix and graph when morph operation (2,3) applied.
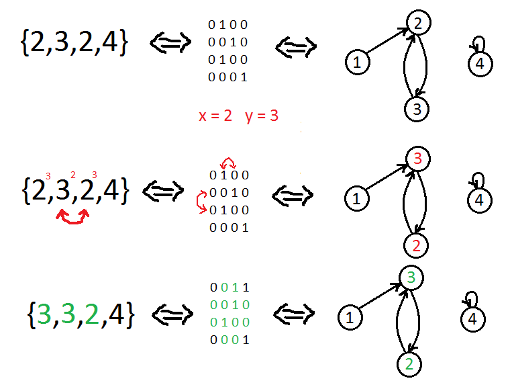
Possibility to swap two indexes makes possible to renumber vertices in any way. It means that one graph can be reached from other if and only if they are isomorphic! So if we count the number of non-isomorphic graphs we'll get required number of equivalence classes. Limitation on outgoing degree(=1) makes it possible to count this number in polynomial time.
Everyone knows that this graphs look as several suns (each component is cycle with some trees connected to its vertices). 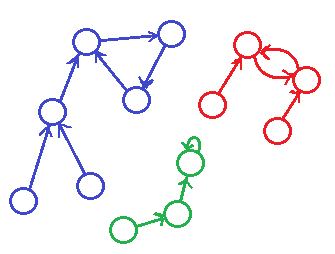
First step is to count the number of rooted trees(with no more than k childs in each vertex). It's not very hard, you just need to remember not to count isomorphic ones few times, consider rooted tree as unordered list of rooted trees.
Next step is to count the number of non-isomorphic suns. If we consider sun as ordered list of rooted trees(with number of childs in root at most k-1), the only mistake that will occur, is that two lists should not be counted twice if they are cyclic shift of each other. If you are familiar with Burnside's lemma you know how to fix it. Here is just a simple case, you can count the number of different strings when you know the number of all.
//all[i] - number of all strings.
//g[i] - number of different strings without lesser period (two strings are equal if one is cyclic shift of another).
//res[i] - number of different strings (two strings are equal if one is cyclic shift of another).
foreach(i) {
g[i] = all[i]
foreach(j < i : i % j == 0) g[i] -= g[j] * j;
g[i] /= i //all strings here have period i and each is counted i times
}
foreach(i) {
res[i] = 0;
foreach(j <= i : i % j == 0) res[i] += g[j];
}
In this problem you also need to remember sizes of everything, so it adds one more parameter size to all arrays.
The final part is to collect suns in whole graph, same as in tree counting need to consider graph as unordered list of suns.
The fact that no one could solve this problem in round time made me sad, but I hope you like this problem and will solve it even without this editorial :)
| Name |
|---|









