Unlike other blogs, I don't have any recent event to be proud of. But still... Ask me anything!
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3650 |
| 2 | Benq | 3582 |
| 3 | Geothermal | 3570 |
| 3 | orzdevinwang | 3570 |
| 5 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3532 |
| 8 | Radewoosh | 3522 |
| 9 | Um_nik | 3483 |
| 10 | jiangly | 3468 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 163 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
Hello, Codeforces! Or, as we like to say in Romania: Sus Sus Sus, ca la Strehaia tată!
I am glad to finally invite you to participate in Codeforces Round 875 (Div. 1) and Codeforces Round 875 (Div. 2), which will start on May/28/2023 17:35 (Moscow time). In both divisions, you will be given 6 problems and 2 hours and 30 minutes to solve them.
The problems were authored and prepared by Andrei_ierdnA, Doru, Gheal, IacobTudor, LucaLucaM, RedstoneGamer22, SlavicG, Sochu, alecs, andrei_boaca, anpaio, lucaperju, valeriu and me ( tibinyte ).
I would like to thank:
- errorgorn, for his wonderful coordination.
- irkstepanov for further help with logistics of organization.
- Alexdat2000 for russian translation.
- alin_gb18, rsj, dario2994
jampm, Psychotic_D, prvocislo
cristi_tanase, atodo, BucketPotato
Moolamp, magnus.hegdahl, Gary2005
Geanina_the_Great, 555, PurpleCrayon
Um_nik, gamegame, conqueror_of_tourist, penguinhacker, AlexLorintz, lucri, _Vanilla_, Vladithur, status_coding, Luci_badea1000, bycicle, myvaluska for testing the round and providing useful feedback.
- freak93 for no morning refreshment.
- MikeMirzayanov for great platforms, codeforces and polygon!
Scoring Distribution
div 2: $$$500-750-1250-1750-2500-3000$$$
div 1: $$$500-1000-1750-2250-3000-3500$$$
The editorial has been published here!
And here are our winners!
| # | Div 1 | Div 2 |
|---|---|---|
| 1 | Ormlis | kotrin |
| 2 | 1a2b3c4 | CLOCKS_PER_SEC |
| 3 | dorijanlendvaj | IHatePaiu |
| 4 | tourist | Lihwy |
| 5 | Radewoosh | VietCek |
To all law authorities, this is an admission of guilt.
Today I competed in Codeforces Round 870 (Div. 2) and I made the unethical move of copying the solution of problem B from some telegram channel. I was foolish to do such a dick move and would like to publicly apologise for my actions.
I would request to be disqualified ( or receive a negative rating change ) because I definitely don't deserve my +11 delta. There are lots of people who worked hard in this contest, but still got a negative rating change.
Cordially,
tibinyte
The Cartesian Tree is a useful concept for solving some problems which revolve mainly about thinking of the range of maximality of elements. It also provides a sort of "persistance" to the algorithm of monotonic stack, if you will. In this blog, we will learn what a Cartesian Tree is, how to construct one and solve some related problems to strengthen our understanding. Let's begin!
What is a Cartesian Tree?
Let's consider an array $$$a$$$ where all values are distinct. The Cartesian Tree for the array $$$a$$$ is a binary labeled tree build recursively from the function $$$get(l,r)$$$ which constructs our desired tree from the subarray $$$l...r$$$.
Now let's define $$$get(l,r)$$$
First root the tree at index $$$i$$$ such that $$$a_i = min(a_l,a_{l+1},...,a_r)$$$. Note that because all values are distinct, $$$i$$$ will always be unique.
The aforementioned index will become the root of the Cartesian Tree. It's left and right subtrees will be recursively generated by $$$get(l,i-1)$$$ and $$$get(i+1,r)$$$ respectively. If $$$i=r$$$ we will ignore the right subtree, if $$$i=l$$$ we will ignore the left subtree.
As an example, consider $$$a=[9,3,7,1,8,12,10,20,15,18,5]$$$. After calling $$$get(1,11)$$$, we get the following tree:
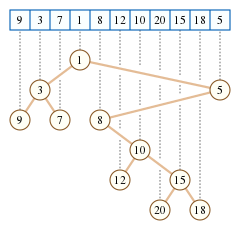
By construction, the Cartesian Tree for an array $$$a$$$ where all values are distinct is always unique. Usually, when there can be repeating values, we will construct the Cartesian Tree in the same manner as before, but we will build it from the pairs {$$$a_i, i$$$}.
The above process can be easily simulated for building a Cartesian Tree in $$$O(nlogn)$$$ using a range minimum query.
Properties of the Cartesian Tree
- Heap: It has a min/max heap structure
- Corollary: Let $$$S_i$$$ be a set where $$$x \in S_i$$$ if and only if there exists $$$1 \le l \le i \le r \le n$$$ such that $$$min(l...r)=x$$$. If we traverse the path from node $$$i$$$ to the root, we will get all values in $$$S$$$ in decreasing order.
- Inorder Completeness: Each subtree represents a range in the original array
- Equivalence to RMQ: Consider $$$2$$$ nodes $$$(i,j)$$$. Let $$$x$$$ be their lca in the Cartesian Tree. We can show that $$$x = min(i...j)$$$.
By the previous claim, we can show that $$$min(i...j)$$$ will be an ancestor of both $$$i$$$ and $$$j$$$. It's easy to see the value at their lca is at most $$$min(i...j)$$$ and looking at the previous claim again, we conclude that their lowest common ancestor is $$$min(i...j)$$$.
Note that by using the last claim we can easily support range minimum query operations on the Cartesian Tree.
Also note that the second claim allows us to build a cartesian tree in $$$O(n)$$$, we can find the parent of each index using monotonic stacks.
Yet Another Array Counting Problem
Let's start with a problem authored by my friend Gheal.
This problem asks us, given an array $$$a$$$, to count the number of arrays $$$b$$$ such that for any subarray, the position of the maximum value is the same in both arrays, given that if there are multiple maximums, we take leftmost. We can easily note that this is equivalent to counting arrays $$$b$$$ for which their Cartesian Tree has the same structure as the Cartesian Tree for $$$a$$$.
And here goes the solution, let $$$dp_{i,j}$$$ hold the number of arrays $$$b$$$ that yield the same Cartesian Tree as the subtree of node $$$i$$$ and the attributed value for the node $$$i$$$ is at most $$$j$$$. We can note that our answer is $$$dp_{root,m}$$$. To calculate we either chose the value of our current node to be $$$j$$$ or rely on $$$dp_{i,j-1}$$$. Thus we can get quick tranisitons:
An implementation of this idea can be viewed here.
Comfortably Numb
Let's build the max Cartesian Tree of the input array. Let's see what the task changes to when switching the array to its Cartesian Tree. It turns out we need, for each root to find $$$max(a_{node} \oplus x \oplus y)$$$ where $$$x$$$ is the prefix xor of some node from the left subtree and $$$y$$$ is the prefix xor of some node in the right subtree ( including the current root ). We can precompute prefix xors and iterate over the smaller subtree and the task becomes finding maximum xor pair which can be done with a trie. Since we merged smallest into largest the complexity is $$$O(n \cdot logn \cdot logM)$$$ where $$$M$$$ is the maximum value in the input.
An implementation of this idea can be viewed here
A harder problem, Vaporeon
Since the statement is only available in romanian, I will translate it for you.
Consider an array with $$$a$$$ with only distinct values ( the problem allows repeted elements, but figuring all the details about making the following solution work on repeating values is left as an exercise to the reader ).
We call $$$f(x)$$$ the depth in the Cartesian Tree of index $$$x$$$. We need to tolerate the following $$$2$$$ operations:
Update: $$$swap(a_i,a_{i+1})$$$
Query: range sum on $$$f$$$
Let's reformulate the problem a little. For each index $$$a_i$$$ we will find the largest range where $$$a_i$$$ is maximum. The depth of the Cartesian Tree of some index is now just the number of intervals that pass through this index. Let's see how we can update those intervals when tolerating a swap update.
We will keep $$$2$$$ arrays of treaps $$$l$$$ and $$$r$$$ where the treap at index $$$l_i$$$ holds all the segments that end at $$$i$$$ ( as left endpoint ) and $$$r_i$$$ keeps all segments ending at $$$i$$$ ( as right endpoint ). WLOG assume we are doing $$$swap(a_i, a_{i+1})$$$ and $$$a_i > a_{i+1}$$$. Now we will analyze how $$$l_{i+1},l_{i+2},r_i,r_{i-1}$$$ change after an update:
$$$l_{i+1} = \varnothing$$$
$$$l_{i+2} = l_{i+1} \cup l_{i+2}$$$
$$$r_{i-1} = r_{i-1} \cap [1,2,3,...,a_{i+1}]$$$
$$$r_i = r_{i-1} \setminus [1,2,3,...,a_{i+1}]$$$
With a bit of extra analyzing we can note that all these operations are doable because $$$l$$$ and $$$r$$$ are kept as treaps and we always merge smaller values with larger values. After performing all these operations, all we are left to do is update the range of $$$a_{i+1}$$$ which we can do via binary searching on a segment tree in $$$O(logn)$$$ and inserting the new range in the corresponding treaps.
Since every update we do a split and a merge on the aforementioned treaps and update a single range, the complexity will be $$$O(logn)$$$. And at the same time there are $$$O(1)$$$ modifications in $$$f$$$ so we can update our range sum data structure fast.
An implementation of this idea can be viewed here.
Constellation 3 ( JOISC 2020 )
We are given a binary matrix. It is known that each column of the binary matrix is white for $$$a_i$$$ cells and then it's just black. We are also given some points with coefficients and are asked to activate a subset of points with maximal cost such that no $$$2$$$ points can see eachother. We consider $$$2$$$ points being able to spot each other iff there exists a black reactangle containing both.
Let's say we took a star on the same Y-coordinate as "smallest" black column ("tallest" building). We can notice that this would imply a restriction of the type "from now on we are only allowed to take stars that are at most $$$a_i$$$ units tall". This is because we will always be able to see that star otherwise.
It turns out this observation is enough for a polynomial solution based on tree DP. This way, we build the min Cartesian Tree and let $$$dp_{i,j}$$$ be the maximum cost of a subset consisting only of nodes from the subtree of $$$i$$$ and my restriction forces me to only take stars at most $$$j$$$ units tall. Transitions are very easy, we can just decide weather we take a star on current column or not. As a detail, if we don't take any star, at least one of the children needs to go at most $$$a_i$$$ units tall restriction, because we would see the 2 stars because they would both pass through $$$i$$$. For a better understanding of this solution, I recommend reading my code.
To achieve a faster solution we must exploit the Cartesian Tree and reduce the problem to something else. The magic reduction uses the corollary of the heap property. Thus we can find that each star's visibility can be expressed as a path from its columns node to the root in the Cartesian Tree. What's more exciting is using the fourth propriety, one can note that $$$2$$$ stars intersect iff their paths intersect, because they can both see the minimum in their range, meaning they can see everything else.
Thus our problem is reduced to chosing some disjoint chains in a tree such their coefficient sum is maximum. Fun fact, this new problem appeared on infoarena before and can be viewed here.
To solve it we just keep in $$$dp_i$$$ the maximum coefficient sum such that all used chains are fully included in the subtree of $$$i$$$. To calculate it we consider each chain that ends in node $$$i$$$ and try to include it in our solution. We need to add all $$$dp$$$ values that are directly attatched to the used chain, which can be done using a bit or any data structure that can support sum on chains with point updates.
For finding the chains we can just use binary lifting, thus our final time complexity is $$$O(nlogn)$$$.
An implementation of this idea can be viewed here.
And last but not least, thanks to Gheal, valeriu, SlavicG for reviewing this blog.
Hello, codeforces!
In my last round, that is CodeTON Round 3, I set a problem no one could solve in the competition. It somehow displays as $$$2100$$$, which I think is not accurate? Can someone review this, please ( MikeMirzayanov ) ?
It's strange as $$$G$$$ is rated as $$$3300$$$.
UPD: fixed
Hello, Codeforces! Or, as we like to say in Romania: Nu îmi amintesc să fi adresat întrebări, Codeforces!
I am glad to finally invite you to participate in CodeTON Round 3 (Div. 1 + Div. 2, Rated, Prizes!), which will start on Nov/06/2022 17:35 (Moscow time). You will be given 8 problems and 2 hours and 30 minutes to solve them. It is greatly recommended to read all the problems, statements are short and straight to the point.
I would like to thank:
- Artyom123 for prodigious coordination.
- AquaMoon, mejiamejia, ugly2333, Ecrade_ for huge help in preparation and authoring one of the tasks.
- errorgorn for being a VIP-tester.
- Lemur95, Gheal, Perpetually_Purple, Everule, IacobTudor, andrei_boaca, lucri, AlperenT, Kuroni, prabowo, lis05, Alon-Tanay, jeroenodb, Juve45, denis2111, Brodicico, Fanurie, huangzirui, satyam343, tfg, Sugar_fan, SlavicG, Vladithur,KrowSavcik, kevinxiehk, sharkycode,Alan, TimDee, Rhodoks, dannyboy20031204,TomiokapEace, Qingyu, lxlxl, ChthollyNotaSeniorious,PinkieRabbit, jerryliuhkg, valeriu, Chenyu_Qiu, jampm, izlyforever, njupt_lyy, RUSH_D_CAT,azureAmarantine, Erkhemkhuu, wh030115,ak2006, dorijanlendvaj, spookywooky, arvindf232, absi2011, AlexLorintz for testing the round and providing invaluable feedback.
- freak93 for morning refreshment.
- MikeMirzayanov for great platforms, codeforces and polygon!
Scoring Distribution: 500-750-1250-1750-2250-2500-3250-3500
The editorial has been published here!
And here are our winners!
- Benq
- zh0ukangyang
- WYZFL
- MagicalFlower
- feecIe6418
- QuietBeautifulThoughts
- p_b_p_b
- conqueror_of_tourist
- jiangly
- tourist
And here is the information from our title sponsor:

Hello, Codeforces!
We, the TON Foundation team, are pleased to support CodeTON Round 3.
The Open Network (TON) is a fully decentralized layer-1 blockchain designed to onboard billions of users to Web3.
Since July, we have been supporting Codeforces as a title sponsor. This round is another way for us to contribute to the development of the community.
The winners of CodeTON Round 3 will receive valuable prizes.
The first 1,023 participants will receive prizes in TON cryptocurrency:
- 1st place: 1,024 TON
- 2–3 places: 512 TON each
- 4–7 places: 256 TON each
- 8–15 places: 128 TON each
- …
- 512–1,023 places: 2 TON each
We wish you good luck at CodeTON Round 3 and hope you enjoy the contest!
Since goals are very important in any individual's life, I decided to set a goal for myself. The target is to set 100 problems until I quit cp.
Current progress: 40
| # | Date | Comments | Feedback | |||
|---|---|---|---|---|---|---|
| 1 | July 2021 | Summer 2021 Round 1 | First problem I ever set. It asks you to find the number of bubble sort iterations to sort a given array | Good Bad | ||
| 2 | July 2021 | Summer 2021 Round 1 | This problem is a very standard problem which asks to find sum of gcds across all subarrays | Good Bad | ||
| 3 | July 2021 | Summer 2021 Round 1 | This is a quite ok digit dp problem which asks finding the number of numbers s.t. the maximum frequency of some digit — minimum frequency of some digit = $$$k$$$, where $$$k$$$ is given | Good Bad | ||
| 4 | July 2021 | Very standard problem that asks to find how many subsets of $$$a$$$ are anagrams of $$$b$$$ | Good Bad | |||
| 5 | July 2021 | Summer 2021 Training round | Very standard problem about stirling numbers of the second kind | Good Bad | ||
| 6 | July 2021 | Summer 2021 Training round | Very standard problem asking for sum of gcds across all arrays of length $$$n$$$ and values in range $$$[1,m]$$$ | Good Bad | ||
| 7 | August 2021 | Summer 2021 Round 2 | Problem asking for number of subarrays with given median | Good Bad | ||
| 8 | August 2021 | Summer 2021 Round 2 | Problem asking for number of subarrays such that if it contains a color, it must contain every color of that kind | Good Bad | ||
| 9 | November 2021 | Autumn 2021 Round 2 Div 2 | A simple greedy problem | Good Bad | ||
| 10 | November 2021 | Autumn 2021 Round 2 Div 1 | I am only a coauthor in this task. The initial problem idea was by Gheal. A quite standard problem on PIE | Good Bad | ||
| 11 | December 2021 | Autumn 2021 Training round | This problem is a math problem that turned into a troll problem with partial scoring. I don't take credit for its idea, only for making it appear in a contest :clown: | Good Bad | ||
| 12 | December 2021 | Autumn 2021 Training round | Educational problem on d&c dp optimization | Good Bad | ||
| 13 | January 2022 | Winter 2022 Round 1 Div 1 | A nice problem, but my sqrt optimizations were just overkill since very simple solutions were using just PIE. I felt bad after finding out all my work optimizing the dp calculations was useless :( | Good Bad | ||
| 14 | February 2022 | CookOff | You set the cancer dp I couldn't solve. First and hardest problem I set on codechef | Good Bad | ||
| 15 | March 2022 | Lunchtime | A quite simple problem about both FFT and PIE. Since I didn't know FFT when I submited this problem on codechef, I'd like to mention Um_nik for improving my initial solution | Good Bad | ||
| 16 | March 2022 | Spring 2022 Round 1 Div 1 | It's a quite simple dp problem with an optimization | Good Bad | ||
| 17 | March 2022 | Spring 2022 Round 1 Div 2 | Quite straightforward couting problem with sieve optimization | Good Bad | ||
| 18 | March 2022 | Spring 2022 Round 1 Div 2 | Quite straightforward problem on monotonic stack | Good Bad | ||
| 19 | April 2022 | Starters 35 | Very cancer dp... It's good to make your enemies hate you more tho... | Good Bad | ||
| 20 | April 2022 | Starters 34 | I think it's one of my best easy problems | Good Bad | ||
| 21 | July 2022 | Lunchtime | Very similar statement to the one in Mex Pairs. Here we write an obvious dp and optimize it in a very interesting way | Good Bad | ||
| 22 | July 2022 | Round #804 | First problem I set on codeforces. My initial solution was $$$O(vmax \cdot log^2)$$$, but thanks to valeriu, it was reduced to $$$O(vmax \cdot log)$$$. I think it's one of my best problems | Good Bad | ||
| 23 | November 2022 | Round 3 | In my opinion, it's a very good D2B problem, solution combines a simple observation with a not so trivial optimization to keep the balance | Good Bad | ||
| 24 | November 2022 | Round 3 | I don't know why this problem was hated in the rate problem section, I think it's a good task that requires both some thinking and implementation | Good Bad | ||
| 25 | November 2022 | Round 3 | This task was added one day before the competition. It looked a good difficulty jump from C, but the distance to E was a bit too large. I apologize for this | Good Bad | ||
| 26 | November 2022 | Round 3 | After realizing how to compute the cost in a smart and flexible way, you can easily use a BIT to solve it | Good Bad | ||
| 27 | November 2022 | Round 3 | I think it's one of the best tasks in the contest, there are lots of solutions to it, mostly all at the same difficulty level. There also exists a $$$O(nlog^2n)$$$ solution, which I have implemented, but we used the $$$O(n^2)$$$ version to fit for $$$F$$$ position | Good Bad | ||
| 28 | November 2022 | Round 3 | It has a hidden refference, but leaving that behind, I think it's a quite nice counting task, and the solution is very unexpected | Good Bad | ||
| 29 | November 2022 | Round 3 | First problem I set on codeforces that didn't have any solves during the official contest. It is supossed to be a hard problem with a quite long implementation, but looking at upsolving submissions, implementation can actually be quite short :) | Good Bad | ||
| 30 | March 2023 | Finally setting on codechef again :) Yet another counting problem that almost went unsolved ( which is very surprising ). Am I too evil to ask variable mod FFT? Do people template variable mod FFT? I don't know. Orz jeroenodb first and only solve to this problem xD | Good Bad | |||
| 31 | May 2023 | A problem I created because we desperately needed a problem for D2B position. I don't think it's great but not bad either. | Good Bad | |||
| 32 | May 2023 | A problem that was intended to be in CodeTON Round 3, but we didn't need it there so we used it here. I came up with this problem while I was in car xD | Good Bad | |||
| 33 | August 2023 | Junior challenge 2023 | Best statement of 2023. Find sum of $$$choose(n,i) \cdot i^k$$$, $$$n \le 10^9, k \le 5000$$$ | Good Bad | ||
| 34 | August 2023 | Junior challenge 2023 | This problem was intended to be in CodeTON round 3 as D, but was removed few days before the competition. This version is however buffed. | Good Bad | ||
| 35 | October 2023 | RCPCamp 2023 Iasi day | This shares a similar statement to Doping, but is much easier. | Good Bad | ||
| 36 | December 2023 | Codeforces Round 915 (Div. 2) | Initial name was Adam Lying Face :( | Good Bad | ||
| 37 | December 2023 | Codeforces Round 915 (Div. 2) | I was expecting this to be as hard as E | Good Bad | ||
| 38 | December 2023 | Codeforces Round 915 (Div. 2) | Used to have some funny refference and a nice drawing but some magician removed both of them. | Good Bad | ||
| 39 | December 2023 | Codeforces Round 915 (Div. 2) | Was intended to be D1B in round #875. We ended up removing it because it was too hard. | Good Bad | ||
| 40 | December 2023 | Stelele informaticii 2023 | Probably D1B~C | A rejected proposal from round 875. | Good Bad |
A — Indirect Sort
Authors: mejiamejia, Ecrade_
We claim that we can sort the array if and only if $$$a_1 = 1$$$.
Necessity
We can notice that index $$$1$$$ cannot be affected by any swap operation.
Let's see what happens to the value $$$1$$$. According to the definition of the operation, it can either increase or be swapped. In order to be increased, there must exist some $$$k$$$ such that $$$1 > a_k$$$, but since $$$1$$$ is the minimum possible value, it will never be true as other values in array $$$a$$$ can only increse as well. Since index $$$1$$$ can not be affected by a swap operation and $$$a_1>1$$$, we conclude that if $$$a_1 \neq 1$$$, the answer is No.
Sufficiency
Let's focus on the second operation. Since we have $$$a_1 = 1$$$, we can always choose $$$i=1$$$ and the operation then turns into picking some pair $$$2 \le j < k \le n$$$ and swapping $$$a_j$$$ with $$$a_k$$$. It's trivial to see we can always sort with such an operation.
B — Maximum Substring
Author: tibinyte
Considering that if we want to find the max value of $$$x \cdot y$$$, then the whole string is the best to calculate, for it $$$0$$$ s and $$$1$$$ s are the max.
Then considering $$$x \cdot x$$$ and $$$y \cdot y$$$ : what we need to do is to calculate the max continuous number of $$$0$$$ or $$$1$$$, compare its square to the first condition, then take the bigger one as the answer.
C — Complementary XOR
Author: tibinyte
For each operation, the interval changed by a sequence and b sequence is complementary, so you must judge whether all $$$[a_i=b_i]$$$ are the same at the beginning. If they are different, you can't have a solution.
Now, if $$$a = \neg b$$$, we can do an operation on $$$a$$$ and have $$$a=b$$$. Now suppose $$$a_i=b_i=1$$$ for some $$$i$$$ and try to make $$$a_i=b_i=0$$$ without changing anything else. If $$$i>1$$$, then this is very simple, we can just do an operation with $$$(1,i)$$$ and an operation on $$$(1,i-1)$$$. If $$$i=1$$$ we can make $$$(1,n)$$$ and $$$(2,n)$$$. Since $$$n>1$$$, this can always be done, thus we found a solution using $$$2 \cdot n + O(1)$$$ operations. To optimize it to only use $$$n + O(1)$$$ operations, note that we only care about the parity of the number of operations did at any index.
D — Count GCD
Author: tibinyte
We can notice that if for some $$$2 \le i \le n$$$, $$$a_{i-1}$$$ is not divisible by $$$a_{i}$$$, then the answer is $$$0$$$. Else, note that all the prime factors of $$$a_1$$$ are also prime factors in all the other values. Thus after factorizing $$$a_1$$$ we can quickly factorize every other value.
Now let's find the number of ways we can select $$$b_i$$$ for every $$$i$$$. The answer will be the product of these values since each position is independent. It's easy to see that there is only one way to select $$$b_1$$$, that is $$$a_1$$$. Now for $$$i > 1$$$ we need to find the number of values $$$x$$$ such that $$$gcd(a_{i-1},x)=a_i$$$. Let $$$x=a_i \cdot k$$$, we can rephrase as $$$gcd( \frac{a_{i-1}}{a_i} \cdot a_i, a_i \cdot k) = a_i$$$, which is also equivalent to $$$gcd( \frac{a_{i-1}}{a_i}, k) = 1$$$. We have $$$k \le \frac{m}{a_i}$$$, thus the task reduces to a simple principle of inclusion-exclusion problem.
Time complexity $$$O(2^9 \cdot 9 \cdot log + \sqrt{m})$$$ per testcase.
E — Bracket Cost
Author: tibinyte
Let $$$a_i=1$$$ if $$$s_i=($$$, $$$a_i=-1$$$ if $$$s_i=)$$$ and $$$b_i$$$ be the prefix sum of $$$a_i$$$.
Theorem: the cost of $$$s[l+1,r]$$$ is $$$max(b_l,b_r)-min(b_l,b_{l+1},...,b_r)$$$
Necessity: after one operation, $$$max(b_l,b_r)-min(b_l,b_{l+1},...,b_r)$$$ decrease at most one.
Sufficiency: If $$$b_l<b_r$$$, we can do operation 2, add a right bracket at the end of string.
If $$$b_l>b_r$$$, we can do operation 2, add a left bracket at the beginning of string.
If $$$b_l=b_r$$$, assume x be the largest x that $$$b_x=min(b_l,b_{l+1},...,b_r)$$$, then $$$s_{x+1}=($$$, so we can do operation 1, cyclic shift $$$s[l,x+1]$$$ to right.
Under any condition, $$$max(b_l,b_r)-min(b_l,b_{l+1},...,b_r)$$$ decrease one after one operation.
We can use binary index tree to calculate $$$max(b_l,b_r)$$$ and $$$min(b_l,b_{l+1},...,b_r)$$$.
F — Majority
Author: tibinyte
First off, let's try to reduce the given operation to a simpler form. We claim that if it is possible to make the string $$$111...111$$$ using the specified operation, we can make it $$$111...111$$$ by doing the following new operation : Select two indices $$$(i,j)$$$ such that the substring $$$s_{i...j}$$$ looks like this $$$111..100...001...111$$$ and make it all one. The proof is just to show that if we can perform operation $$$(i,j)$$$, then it must exist some substring of $$$s_{i...j}$$$ respecting the propriety of the new operation.
Let $$$dp_{i,j}$$$ be the number of binary strings of length $$$i$$$ that in the final form ( after no more operations can be made ) begin with a prefix full of ones of length $$$j$$$. For transitions, we have to iterate through the length of the next $$$0$$$ sequence and the length of the fixable prefix right after it ( such that we cannot perform an operation to make a bigger prefix, because that would break the definition ), but there is one problem -- we cannot compute $$$dp_{i,i}$$$ using any recurrence relation. Fortunately, we can compute it by subtracting the ways we get roadblocks, because, by definition $$$dp_{i,i}$$$ can be turned into $$$111...111$$$ which doesn't have any roadblocks at all. This is $$$O(n^4)$$$ if implemented naively, but one can optimize it to $$$O(n^2)$$$ by keeping prefix sums over prefix sums.
Challenge: Solve the problem in $$$O(nlog^2)$$$ or $$$O(nlog)$$$ ( modulo is prime )
G — Doping
Author: tibinyte
Consider a permutation $$$p$$$ that lexicographically smaller than given permutation, assume the first different position is $$$k$$$, if we fix $$$p_k$$$, the remaining numbers $$$a_{k+1},a_{k+2},...,a_n$$$ can be arranged in any order. Denote $$$S$$$ as the set of remaining numbers. Let $$$m$$$ be the number of consecutive pairs, $$$m=|{x|x \in S,(x-1) \in S\cup{p_k} }|$$$, $$$p_k$$$ is included because it is possible that $$$p_{k+1}=p_k+1$$$. Fix the number of positions that $$$p_i=p_{i-1}+1$$$, this consumes some consecutive pairs, the remaining consecutive pairs should not increase the number of positions. Define a sequence $$$p$$$ good if and only if it has no $$$i$$$ that $$$p_i=p_{i-1}+1$$$.
Consider $$$dp[i][j]$$$ = number of good arrangements of $$$i$$$ values with $$$j$$$ consecutive pairs. Consider one consecutive pair, if it is the only wrong pair, the number of values decrease by one and this situation should be excluded, otherwise this pair can be ignored, so $$$dp[i][j]=dp[i][j-1]-dp[i-1][j-1]$$$, with boundary $$$dp[i][0]=i!$$$. After enumrating $$$k$$$, let $$$S'={a_k,a_{k+1},...,a_n}$$$, $$$p_k$$$ is chosen from $$$S'$$$ and $$$p_k<a_k$$$. Assume $$$p_k=x$$$, if $$$x-1 \in S'$$$, the number of consecutive pairs decrease by one, otherwise it stay the same. Additionally, if $$$x \ne p_{k-1}+1$$$, the number of subarrays increase by one. For every situation, count the number of $$$p_k$$$ and then calculate answer.
Time complexity: $$$O(n^2)$$$.
Since we have to deal with lexicographically smaller condition, it's natural to fix the common prefix $$$i$$$. Now, we can mismatch $$$p_{i+1}$$$ with some of the left values. After that, we are left with permuting the other elements.
Let's say we are trying to find the number of ways to permute the remaining values {$$$a_1,a_2,a_3,...,a_k$$$} such that $$$a_i \neq a_{i+1}-1$$$ for $$$1 \le i < k$$$.
For each $$$i$$$, we define $$$b_i$$$ to be a boolean value denoting the existence of $$$a_i - 1$$$ in set $$$a$$$.
We can formulate the following 2 claims:
- The number of ways to permute array $$$a$$$ only depends on $$$k$$$ and sum of $$$b$$$
- For some pair $$$(i,j)$$$, the number of ways to permute $$$a$$$ starting with $$$a_i$$$ is equal to the number of ways to permute $$$a$$$ starting with $$$a_j$$$ if and only if $$$b_i = b_j$$$
With these observations, we can formulate a $$$dp$$$ solution for counting permutations. Let $$$dp_{i,j,flag}$$$ be the number of ways to permute if $$$k=i$$$, $$$j$$$ is the sum of $$$b$$$, starting with a value with $$$b$$$ value equal to $$$flag$$$. Let's conclude transitions:
- $$$dp_{i,1,true} = dp_{i-1,1,false}$$$
- $$$dp_{i,1,false} = (dp_{i-1,1,true} + dp_{i-1,1,false}) \cdot (i-1)$$$ $$$-$$$ By claim 2, we can think of ending in the minimum value and we are left with another permutation we can transition 2.
- $$$dp_{i,j>1,true} = (dp_{i-1,j-1,true}+dp_{i-1,j-1,false}) \cdot j$$$ $$$-$$$ By claim 1, we can think of an equivalent array $$$a$$$ in which all values with $$$b_i = 1$$$ are left alone. Combining with claim 2, all distributions are equal, and selecting a single value makes the permutation have $$$j-1$$$ values with $$$b_i=1$$$.
- $$$dp_{i,j>1,false} = (dp_{i-1,j,false} + dp_{i-1,j,true}) \cdot (i-j)$$$ $$$-$$$ By claim 2, we can select any value with $$$b_i=0$$$ and combining with claim $$$2$$$, we can select the first value in the last chain.
Let $$$sum$$$ be the sum of $$$b$$$.The number of ways to permute $$$a$$$ such that it respects the given demands, is $$$dp_{k,sum,true} + dp_{k,sum,false}$$$. Now the number of ways to permute $$$a$$$ with $$$t$$$ positions such that $$$a_i \neq a_{i+1}-1$$$ is $$$\binom{k-sum}{t-sum} \cdot (dp_{k,t,true} + dp_{k,t,false})$$$. This is because we can choose the values that contribute, $$$sum$$$ of them are always contributing, so we are left with choosing $$$t-sum$$$ values out of $$$k-sum$$$ possibilities.
Now thinking about the values we missmatch $$$p_{i+1}$$$ with, looking at claim $$$2$$$, a lot of values are equivalent. We can count each value type separately since there are $$$O(1)$$$ types, and have a $$$O(n)$$$ complexity to update the results accordingly. Also be careful with the case where a past range of consecutive values is continued after the missmatch. It's easy to handle this because $$$p'_{i+1}$$$ is fixed and we can count it independently in $$$O(n)$$$.
Thus we have achieved $$$O(n^2)$$$ total time complexity
H — BinaryStringForces
Author: tibinyte
We call a maximal sequence of $$$0$$$ a $$$0$$$ block, a maximal sequence of $$$1$$$ a $$$1$$$ block.
For each $$$i$$$, store some disjoint intervals with the following property:
For each $$$j$$$ that $$$i<=j$$$ and $$$s[j]=1$$$, j is in one of the intervals if and only if $$$(i,j)$$$ is a good substring.
We can prove the number of intervals for each $$$i$$$ is $$$O(\log n)$$$.
Let's start from $$$(i,i)$$$ to $$$(i,n)$$$, and consider when. good substring become bad and bad substring become good.
Assume we are at $$$(i,j)$$$.
If it is a good substring and ending with 1, it become bad when it meet a longer 0 block, so we get one interval and go to a bad substring ending with 0.
If it is a bad substring and ending with 0, suppose the next 1 is at k, then the next good intervals start at the smallest j' with three properties: (1) $$$(k,j')$$$ is good
(2) $$$s[j']=1$$$
(3) $$$(k,j')$$$ is not shorter than the last 0 block.
Proof: Property 2 is obvious because we only care about substrings ending with 1.
If $$$(k,j')$$$ is shorter than the last $$$0$$$ block, it is impossible to change this $$$0$$$ block, so $$$(i,j')$$$ is bad.
If $$$(k,j')$$$ is bad, if it starts with a 1 block $$$(k,j")$$$ not shorter than the last $$$0$$$ block after some operations, then $$$j"$$$ is smaller than $$$j'$$$ and has those three properties, otherwise it is impossible to change the last $$$0$$$ block.
If it has all three properties, in substring $$$(i,j')$$$, $$$(k,j')$$$ is good and can change the last $$$0$$$ block $$$1$$$, and then change $$$(i,j')$$$ to $$$1$$$, so we go to a good substring ending with 1.
When good substring become bad, the length is doubled, so the number of intervals for each i is $$$O(logn)$$$.
To know when good substring become bad ,for every 0 block $$$(j,k)$$$,if $$$(j,k)$$$ is longer than $$$(i,j-1)$$$, then $$$(i,k)$$$ is bad, we can preprocess those i in $$$O(n)$$$.
To know when bad substring become good, we go with $$$i$$$ from $$$n$$$ to $$$1$$$ and for each $$$i$$$, search in $$$O(\log n)$$$ intervals $$$O(\log n)$$$ times.
So we get those intervals in $$$O(n\log^2 n)$$$
Now we can check each substring ending with $$$1$$$ is good or not. Do the above algorithm on the reversed string, so we can check each substring starting with 1 is good or not. But we can not check substring starting and ending with 0.
Suppose $$$(i',j')$$$ is the longest $$$0$$$ block in $$$(i,j)$$$, then $$$(i,j)$$$ is good if at least one of $$$(i,i'-1)$$$ and $$$(j'+1,j)$$$ is good and not shorter than $$$(i',j')$$$.
Proof: After changing the longest $$$0$$$ block, we can change all other $$$0$$$ blocks. So for any substring, it is good if and only if we can change its longest $$$0$$$ block.
If $$$(i,i'-1)$$$ is good and not shorter, it can change $$$(i',j')$$$, so $$$(i,j)$$$ is good.
If $$$(i,j)$$$ is good assume the longest 0 block is changed from left. So after some operations in $$$(i,i'-1)$$$, there is a substring $$$(k,i'-1)$$$ become all $$$1$$$ and not shorter than $$$(i',j')$$$. Then $$$(k,i'-1)$$$ can make $$$(i,i'-1)$$$ good as there is no longer $$$0$$$ block.
Similarly, we can prove for $$$(j'+1,j)$$$.
So for each substring, we consider its longest $$$0$$$ block (substrings with no $$$0$$$ are always good). For convenience, if there are multiple maximum, we take the rightmost.
The longest $$$0$$$ block in substrings can be either a $$$0$$$ block in the original string or part of $$$0$$$ block in the original string. We can ignore substring in one $$$0$$$ block, so the longest $$$0$$$ block can only be a prefix or suffix, the number of possible longest $$$0$$$ block is $$$O(n)$$$.
For each possible 0 block $$$(i,j)$$$, assume the longest substring that $$$(i,j)$$$ is the longest $$$0$$$ block is $$$(i',j')$$$, we need to count answer for substring $$$(l,r)$$$ that $$$i' \le l \le i,j \le r \le j'$$$, it is equivalent to count the number of $$$l$$$ that $$$i'\le l \le i-(j-i+1)$$$ and $$$(l,i-1)$$$ is good and the number of $$$r$$$ that $$$j+(j-i+1) \le r \le j'$$$ and $$$(j+1,r)$$$ is good.
Notice that $$$s[i-1]=s[j+1]=1$$$, we can calculate them by above intervals.
We can use persistent segment tree directly or use segment tree or binary index tree after sorting queries. We need $$$O(nlogn)$$$ modifications and $$$O(n)$$$ queries. Thus we have solved our problem in $$$O(n\log^2 n)$$$.
#LeafTON
| Name |
|---|










