There seems to be some confusion reagarding this post being copied from stackexchange, but let me tell you that was my friend who posted it from his fake account without my knowledge, but now i need help genuinely, please provide input if you can.

I am currently working on a heuristic for a problem called the Spanner Sum Problem(NP problem). I'll try and incorporate all the relevant information here, in the blog post so we can have the best of ideas and inputs from your side!

Problem Statement: To find a spanning tree of a graph such that the shortest distances between all node pairs of chord edges related to that spanning tree are as low as possible (related problem statement is: to minimise the edges while keeping the connectivity b/w the nodes as good as possible)

ref:(An edge of a spanning tree is called a branch; an edge in the graph that is not in the spanning tree is called a chord.)

Let's assume we have a Regular Un-Directed Graph G with E edges and V vertices. Let's take an image for reference:

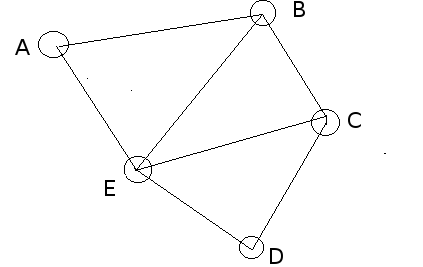
in the above graph, let's count the cost to traverse from one vertex of a chord(according to the spanning tree obtained) to another vertex of that chord. Here for chord AB, A to B takes one edge AB, We can easily observe the rest.

Now say we convert this graph into some(just for demonstration) Spanning Tree. Let's say the resulting spanning tree looks something like this:

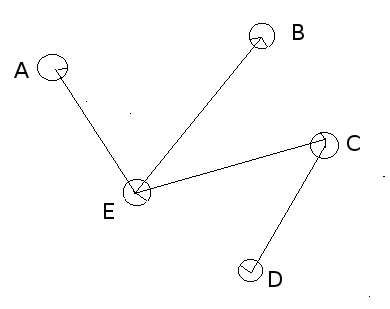
Now we notice that the number of edges to be traversed to reach from A to B(which is a chord), has changed from 1 earlier to 2 now. Same is the case for the pair E to D and B to C where the distance to go from one of these vertices to other has increased. This increase in distance has to be minimised while having as fewer edges as possible(basically a spanning tree), as simple as that.

Let us define the (Minimum) Spanner Sum Problem as follows

For a spanning tree T of G, the spanner-sum is defined by ζ s (T, G) = ∑dT (u, v) where (u, v) ∈ E(G) \ E(T) and dT (u, v) denotes the distance between u and v in T. Then, the minimum spanner-sum of G is defined as ζ s (G) = minζ s (T, G) where the minimum is taken over all spanning trees T of G.

In more layman terms, the spanner sum problem deals with the issue of converting a graph to a tree, removing edges which yield a spanning tree which minimises distances b/w pairs of vertices, trying to keep the distance the same as in the original graph and the spanner sum is the sum of the distances related to all the chords(for some spanning tree) of the graph

We came up with the following heuristic to convert a graph into a spanning tree having minimum spanner sum:

Algorithm

• Begin by finding the smallest cycles and remove one of the edges of that cycle, basically breaking the cycle and going one step nearer to spanning tree. The reason behind finding the smallest cycle first is to have minimum impact on the spanner sum, bcoz when we disconnect an edge from this cycle, the cost added up in the spanner sum for this particular removed edge(chord) would be the length of the cycle found — 1.

Let me illustrate with an elementary isolated example. Take 2 cycles, one of length 3 and other of length 5: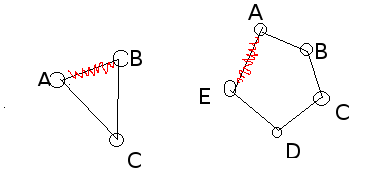

If we remove edge AB, then the distance between A and B increases from 1(**AB** itself) to 2 ( AC -> CB ). In the second case, when we remove edge AE, the distance from A to E increases from 1 (when AE was present) to 4 ( AB -> BC -> CD -> DE )

• Now that we have a cycle, what edge of the cycle to remove?

Now here is where we have made logical(subjective, nonetheless) presumption. It would be great if someone would provide some mathematical backing for the below as we can't seem to think of a way to do so.

Remove the edge where the sum of the degrees of both its vertices is minimum compared to all the other edges in the cycle

Now let's think why we would do so. When you have an edge who's vertices have the least degree, that would mean that this edge is a junction that is connecting LESSER number of places to a lesser number of place, right? If you have an edge who's vertices have a high degree, that would mean that there are several incoming paths to vertex one and are outgoing from vertex 2. If we were to remove this edge, it would have a greater impact of the connectivity of the graph so we wouldn't want to remove it. This is why we would choose the edge whose sum of degree of vertices is minimum.

• Next Step — Mark the rest of the edges of this cycle and don't remove them if encountered in future cycles, basically these have been fixed as a part of the segment tree that we are going to get finally.

Now when you disconnect an edge from a cycle, you mark all the other edges in the cycle. The reason to do this is as follows. Suppose that you encounter one of these edges you encountered in the smaller cycle as a part of a bigger cycle later on and decide to remove one of these. If you were to do so, you would reduce/disturb the connectivity of the smaller cycle edges you had processed before. This would essentially result in your previous calculations being rendered useless.

• Incrementally calculate the spanner sum

The spanner sum is initialised as 0. Now having removed an Edge represented by endpoints V1 and V2, the new length of path b/w v1 and v2 is length of cycle-1. So we have length of cycle-1 added to the spanner sum.

• Repeat until V-1 Edges remain in t*emphasized text*he graph.

This is the basic procedure that needs to be repeated until V — 1** edges exist in the graph. That means that we've formed out spanning tree.

Working out an example

Here's an image where I've worked out an example I'll be explaining below

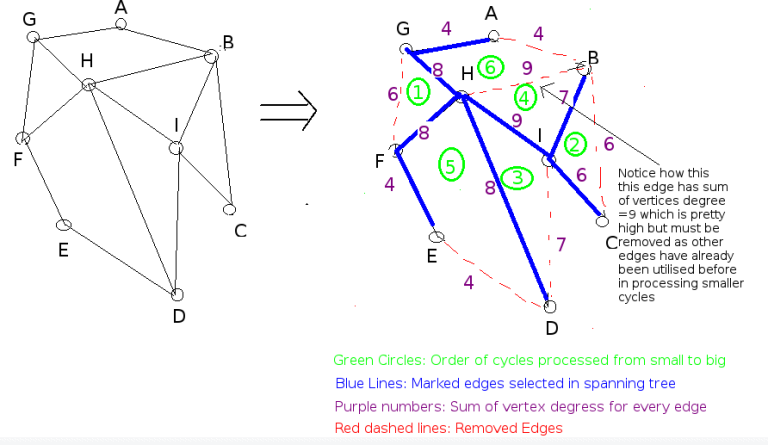
We first with start with the smallest cycles, here of size 3. All the cycles considered are circled in GREEN which indicates the order they were processed in. Cycles of same size my be processed in any order. We check the sum of degrees of vertices of an edge (marked over each edge in PURPLE) and remove the one with the least sum(removed edge marked in RED) as described in the algorithm. If there are multiple edges with the same sum, break the tie arbitrarily. Then, we mark the remaining edges of the cycle in BLUE which will form a part of the spanning tree and cannot be considered for removal if they form a part of a larger cycle later on. Simply repeat this procedure until only V — 1 edges remain in the graph and stop.

Implementation Notes

To find the Smallest cycles, we use an Iterative Deepening DFS where we start with smallest depth, depth 3, to find all the smallest cycles. Once all the cycles of length 3 are over, we increase the depth to 4, 5 and so on.

Once we encounter a cycle, we check the vertex degrees for each edge of the cycle, remove the one with the minimum degree sum, increment the spanner sum with length of cycle — 1 and continue.

We have attempted a sort of buggy but readable implementation. It runs on certain testcases, on some it goes into an infinite loop but we have made a fair attempt and are working on correcting the code as you are reading this :)

Here it is http://ideone.com/KDztVn

Thoughts and Help Required!

This problem is an NP problem as far as we know, and we've come up with this particular heuristic algorithm. However, we can't provide any mathematical backing for our choice of removal edges.

We have done a few tests where we removed the edges with the maximum sum of vertex degrees instead of minimum as we are doing here, and the spanner sum we got in the end was much higher than this algorithm proposed. So we are inclined to believe that this greedy approach of ours seems to work out, in a heuristic sense, by showing that removal of the other extreme edge, the one with max sum of vertex degrees is not yielding a good result.

We're looking from some interesting inputs from your side, proposed improvements or maybe a completely new algorithm itself. We would be highly grateful if anyone of you could provide us direction with a mathematical proof that sort of proves in theory that this algorithm works.

Thanks for the read and looking forward to constructive discussion in the comments. Kindly feel free to point out any mistakes in the post or wherever additional explanation is required!

#include <bits/stdc++.h>
using namespace std;
#define MAX_NUMBER_OF_NODES 10000000
#define endl '\n'
#define f0(i, n) for(int i=0; i<n; i++)
typedef long long int ll;

ll trie[MAX_NUMBER_OF_NODES][2]={0};
ll store[MAX_NUMBER_OF_NODES][2]={0};
ll nxt = 1;
ll count1=0;
// Each row represents a node
// Numbers in that row represent the nxt node to which it is connected
// That number will be our nxt row

void insrt(int n) {
	ll t = 1;
	int z=31;
	for(int i = 0; i < 32; i++) {
		int p = ((1<<z)&n)?1:0;
		//cout<<p;
		z--;
		store[t][p]++;
		//cout<<store[t][p]<<" ";
		if(trie[t][p] == 0) {
			nxt++;
			trie[t][p] = nxt;
		} 
		if(p==0) {
			count1 += store[t][1];
		}
		t = trie[t][p];
	}
}

int main () {
	int t;
	cin>>t;
	while(t--) {
		for(int i=0; i<=nxt; i++) {
			trie[i][0]=0;
			trie[i][1]=0;
			store[i][0]=0;
			store[i][1]=0;
		}
		nxt=1;
		count1=0;
		int n;
		cin>>n;
		int a[n];
		f0(i, n) { 
			cin>>a[i];
			insrt(a[i]);
		}
		//f0(i, 6) insrt (a[i]);
		cout<<count1<<endl;	
	}
	
	return 0;
}

// the following code is a solutoin the problem INVCNT on spoj. // the basic idea is to maintain a trie with count of each node in the trie. // for inversions if we have a 1 at current node then we are sure that the number(which we are inserting //currently) is greater than the other already inserted numbers which have the same prefix as the current //number upto the current node but have 0 at current node. we maintain a count of such nodes or numbers.