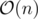You should know only one fact to solve this task: 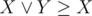 . This fact can be proved by the truth table. Let's use this fact:
. This fact can be proved by the truth table. Let's use this fact: 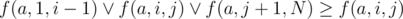 . Also
. Also 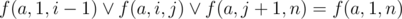 . According two previous formulas we can get that f(a, 1, n) ≥ f(a, i, j). Finally we can get the answer. It's equal to f(a, 1, N) + f(b, 1, N).
. According two previous formulas we can get that f(a, 1, n) ≥ f(a, i, j). Finally we can get the answer. It's equal to f(a, 1, N) + f(b, 1, N).
Time: 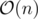
Memory: 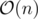
Let's define timeRi as a number of last query, wich repaint row with number i, timeCj – as number of last query, wich repaint column with number j. The value in cell (i, j) is equal amax(timeRi, timeCj).
Time: 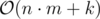
Memory: 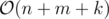
If we have some pair of queries that ri ≥ rj, i > j, then we can skip query with number j. Let's skip such queries. After that we get an array of sorted queries (ri ≤ rj, i > j). Let's sort subarray a1..max(ri) and copy it to b. For proccessing query with number i we should record to ari - 1..ri first or last(it depends on ti - 1) ri - 1 - ri + 1 elementes of b. After that this elements should be extract from b. You should remember that you need to sort subarray a1..rn, after last query.
Time: 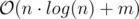
Memeory: 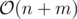
Let's define S[i] as i - th block of S, T[i] — as i - th block of T.Also S[l..r] = S[l]S[l + 1]...S[r] and T[l..r] = T[l]T[l + 1]...T[r].
T is substring of S, if S[l + 1..r - 1] = T[2..m - 1] and S[l].l = T[1].l and S[l].c ≥ T[1].c and S[r].l = T[m].l and S[r].c ≥ T[m].c. Let's find all matches of T[l + 1..r - 1] in S and chose from this matches, witch is equal T.You can do this by Knuth–Morris–Pratt algorithm.
This task has a some tricky test cases:
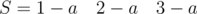 and
and 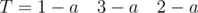 . Letters in the adjacent blocks are may be same.This problem can be solved by the union of adjacent blocks with same letter.
. Letters in the adjacent blocks are may be same.This problem can be solved by the union of adjacent blocks with same letter.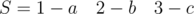 and
and 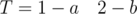 . Count of T blocks are less than 3. Such cases can be proccess singly.
. Count of T blocks are less than 3. Such cases can be proccess singly.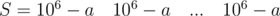 and
and 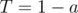 . Answer for this test should be stored at long long.
. Answer for this test should be stored at long long.
Time: 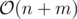
Memory: 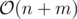
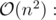
The operation, which has been described in the statement, is cyclic shift of some subarray. Let's try to solve this problem separately for left cyclic shift and for right cyclic shift. Let's define 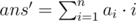 as answer before(or without) cyclic shift, Δans = ans - ans' — difference between answer after cyclic shift and before. This difference can be found by next formulas:
as answer before(or without) cyclic shift, Δans = ans - ans' — difference between answer after cyclic shift and before. This difference can be found by next formulas:
For left cyclic shift:
Δl, r = (al·r + al + 1·l + ... + ar·(r - 1)) - (al·l + al + 1·(l + 1) + ... + ar·r) = al·(r - l) - (al + 1 + al + 2 + ... + ar)
For right cyclic shift:
Δ'l, r = (al·(l + 1) + al + 1·(l + 2) + ... + ar·l) + (al·l + al + 1·(l + 1) + ... + ar·r) = (al + al + 1 + ... + ar - 1) + ar·(l - r)
You can find this values with complexity 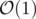 , using prefix sums,
, using prefix sums, 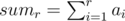 .
.
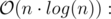
Let's try to rewrite previous formulas:
For left cyclic shift: Δl, r = (al·r - sumr) + (suml - al·l)
For right cyclic shift: Δ'l, r = (ar·l - suml - 1) + (sumr - 1 - ar·r)
You can see, that if you fix l for left shift and r for right shift, you can solve this problem with complexity 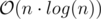 using Convex Hull Trick.
using Convex Hull Trick.
Time: 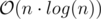
Memory: