I am trying to solve this problem ( https://www.hackerrank.com/contests/hourrank-12/challenges/fair-cut ). The editorial describes D.P approach which I am not able to understand. In the discussion, I saw a greedy approach but I am not able to prove why it works.
Can someone please help me in understanding the D.P approach to this question?
Thanks.








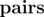 such that
such that 

