(Sorry for my poor English. >_<)

(Sorry for my poor English. >_<)

(Sorry for my poor English. >_<)

First of all, here are some links about CERC2016:

[1] The contest page in CF: https://codeforces.com/gym/101173

[2] The official tutorial: https://cerc.hsin.hr/2016/tasks/cerc2016_presentation.pdf

The text I put below is from page 117 of the official tutorial.

Finally, we'll revise our gap-finding algorithm, not to visit both children when the split would result in two tiles that look the same with respect to intersecting with the polygon. Instead we visit only one children, but create twice as many gaps in that branch. It can be shown that this way we'll only visit $$$O(nm^2)$$$ states. ...

It mentioned that "this way we'll only visit $$$O(nm^2)$$$ states".

I have spent several hours on trying to prove this. However, I can't prove it. And it seems to have some counterexamples.

Maybe it is a counterexample:

Let's assume that $$$m \approx 2 ^ 8 \times 4, n \approx 32$$$. This will make it more convenient to describe the counterexamples.

Let's construct a polygon. It looks like the picture showed below.

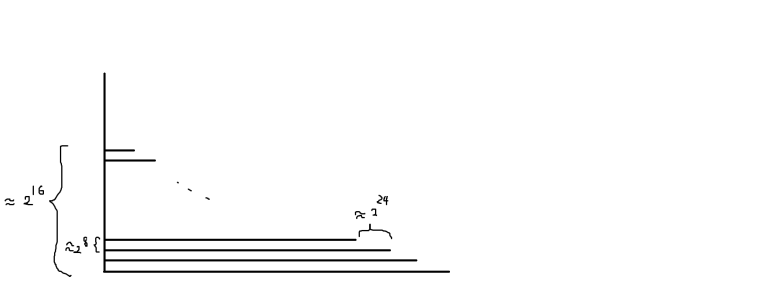
This polygon is made up of many vertical or horizontal sticks. The width of each stick is 1.

Firstly, a vertical stick is put into the leftmost part of the $$$2 ^ n \times 2 ^ n$$$ rectangular grid. Then $$$\approx 2^8$$$ horizontal sticks will be put in while the conditions below are satisfied:

1. The left endpoint of each stick is next to the vertical stick.

2. For two adjacent sticks, the distance between them is about $$$2 ^ 8$$$ and the stick below is $$$2^{24}$$$ longer than the one above.

Let $$$x$$$ be a integer so that $$$x \in [16,24)$$$(approximately).

Given the polygon above and an $$$2^x \times 2^x$$$ rectangular tiling of the plane, there will be $$$O(m)$$$ different tiles with respect to intersection with the polygon. To solve the subtasks bounded by rectangles in the following figure, we need to visit $$$O(m ^ 2n)$$$ states. But don't forget that there're $$$O(n)$$$ valid values for $$$x$$$. So it will be $$$O(m ^ 2n ^ 2)$$$ states to visit.

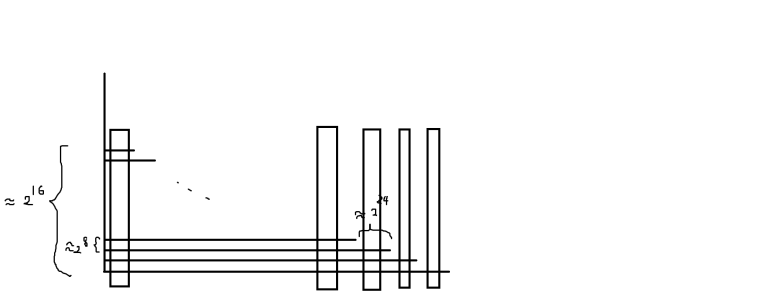
I wonder that whether my counterexample is right and whether there is a proof of the unproven conclusion in the tutorial.

Can anyone help me?

Thank you in advance!

update(2020.10.15)

I think I make the number of visited states to $$$O(n^2m^2)$$$ successfully. However, it's just a theoretical complexity. The algorithm runs really fast.

Here I'll show two datamakers.

$$$n = 30, m = 200$$$

#include <bits/stdc++.h>
#define For(i,a,b) for (int i=(a);i<=(b);i++)
#define fi first
#define se second
#define pb(x) push_back(x)
#define mp(x,y) make_pair(x,y)
using namespace std;
typedef long long LL;
int main(){
	srand(time(NULL));
	int n=30;
	vector <pair <LL,LL> > ps;
	LL c=1<<9;
	for (LL i=0;i<50;i++){
		ps.pb(mp(1,i*c+1));
		ps.pb(mp((1LL<<n)-1-(i<<24),i*c+1));
		int r=c-2;
		ps.pb(mp((1LL<<n)-1-(i<<24),i*c+1+r));
		ps.pb(mp(1,i*c+1+r));
	}
	ps[0].fi--;
	ps.back().fi--;
	printf("%d\n%d\n",n,(int)ps.size());
	for (auto i : ps)
		printf("%lld %lld\n",i.fi,i.se);
	int q=1;
	printf("%d\n",q);
	For(i,1,q)
		printf("%d\n",rand()%9+1);
	return 0;
}

$$$n = 60, m = 256$$$

#include <bits/stdc++.h>
#define For(i,a,b) for (int i=(a);i<=(b);i++)
#define fi first
#define se second
#define pb(x) push_back(x)
#define mp(x,y) make_pair(x,y)
using namespace std;
typedef long long LL;
int main(){
	srand(time(NULL));
	int n=60;
	vector <pair <LL,LL> > ps;
	LL c=1<<25;
	for (LL i=0;i<64;i++){
		ps.pb(mp(1,i*c+1));
		ps.pb(mp((1LL<<n)-1-(i<<54),i*c+1));
		int r=c-2;
		ps.pb(mp((1LL<<n)-1-(i<<54),i*c+1+r));
		ps.pb(mp(1,i*c+1+r));
	}
	ps[0].fi--;
	ps.back().fi--;
	printf("%d\n%d\n",n,(int)ps.size());
	for (auto i : ps)
		printf("%lld %lld\n",i.fi,i.se);
	int q=1;
	printf("%d\n",q);
	For(i,1,q)
		printf("%d\n",rand()%9+1);
	return 0;
}