- Microsoft Q#
You are given a quantum oracle - an operation on N + 1 qubits which implements a function 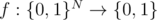 . You are guaranteed that the function f implemented by the oracle is either constant (returns 0 on all inputs or 1 on all inputs) or balanced (returns 0 on exactly one half of the input domain and 1 on the other half).
. You are guaranteed that the function f implemented by the oracle is either constant (returns 0 on all inputs or 1 on all inputs) or balanced (returns 0 on exactly one half of the input domain and 1 on the other half).
There are only two possible constant functions: f(x) = 0 and f(x) = 1. The functions implemented by oracles in the two previous problems (f(x) = xk and 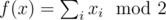 ) are examples of balanced functions.
) are examples of balanced functions.
Your task is to figure out whether the function given by the oracle is constant. Your code is allowed to call the given oracle only once.
You have to implement an operation which takes the following inputs:
- an integer N - the number of qubits in the oracle input,
- an oracle Uf, implemented as an operation with signature ((Qubit[], Qubit) => ()), i.e., an operation which takes as input an array of qubits and an output qubit and has no output.
The return of your operation is a Boolean value: true if the oracle implements a constant function and false otherwise.
Your code should have the following signature:
namespace Solution {
open Microsoft.Quantum.Primitive;
open Microsoft.Quantum.Canon;
operation Solve (N : Int, Uf : ((Qubit[], Qubit) => ())) : Bool
{
body
{
// your code here
}
}
}
| Name |
|---|



