You are looking at the floor plan of the Summer Informatics School's new building. You were tasked with SIS logistics, so you really care about travel time between different locations: it is important to know how long it would take to get from the lecture room to the canteen, or from the gym to the server room.
The building consists of n towers, h floors each, where the towers are labeled from 1 to n, the floors are labeled from 1 to h. There is a passage between any two adjacent towers (two towers i and i + 1 for all i: 1 ≤ i ≤ n - 1) on every floor x, where a ≤ x ≤ b. It takes exactly one minute to walk between any two adjacent floors of a tower, as well as between any two adjacent towers, provided that there is a passage on that floor. It is not permitted to leave the building.
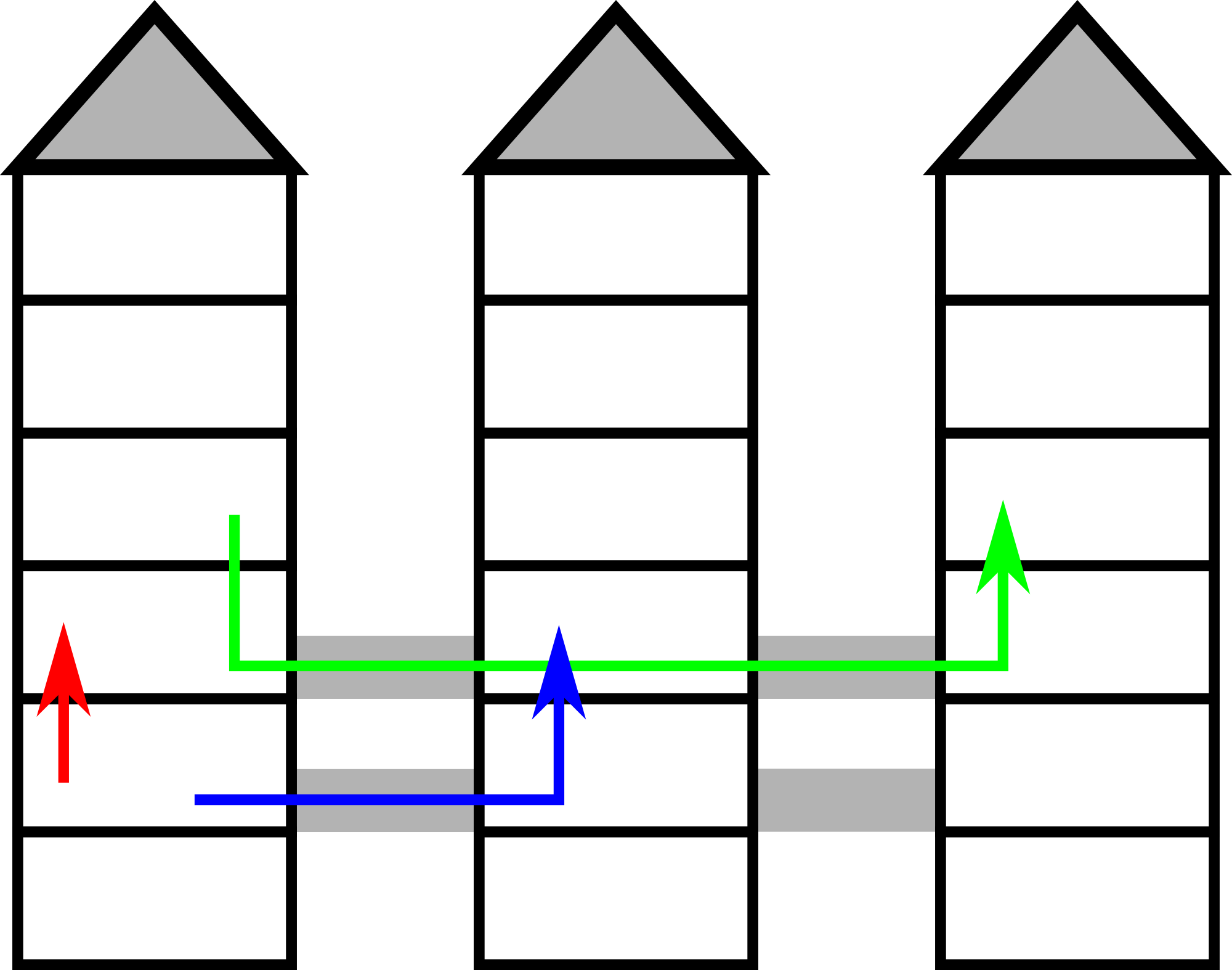
The picture illustrates the first example.
You have given k pairs of locations (ta, fa), (tb, fb): floor fa of tower ta and floor fb of tower tb. For each pair you need to determine the minimum walking time between these locations.
The first line of the input contains following integers:
- n: the number of towers in the building (1 ≤ n ≤ 108),
- h: the number of floors in each tower (1 ≤ h ≤ 108),
- a and b: the lowest and highest floor where it's possible to move between adjacent towers (1 ≤ a ≤ b ≤ h),
- k: total number of queries (1 ≤ k ≤ 104).
Next k lines contain description of the queries. Each description consists of four integers ta, fa, tb, fb (1 ≤ ta, tb ≤ n, 1 ≤ fa, fb ≤ h). This corresponds to a query to find the minimum travel time between fa-th floor of the ta-th tower and fb-th floor of the tb-th tower.
For each query print a single integer: the minimum walking time between the locations in minutes.
3 6 2 3 3
1 2 1 3
1 4 3 4
1 2 2 3
1
4
2
| Name |
|---|




