A tree is an undirected graph with exactly one simple path between each pair of vertices. We call a set of simple paths $$$k$$$-valid if each vertex of the tree belongs to no more than one of these paths (including endpoints) and each path consists of exactly $$$k$$$ vertices.
You are given a tree with $$$n$$$ vertices. For each $$$k$$$ from $$$1$$$ to $$$n$$$ inclusive find what is the maximum possible size of a $$$k$$$-valid set of simple paths.
The first line of the input contains a single integer $$$n$$$ ($$$2 \le n \le 100\,000$$$) — the number of vertices in the tree.
Then following $$$n - 1$$$ lines describe the tree, each of them contains two integers $$$v$$$, $$$u$$$ ($$$1 \le v, u \le n$$$) — endpoints of the corresponding edge.
It is guaranteed, that the given graph is a tree.
Output $$$n$$$ numbers, the $$$i$$$-th of which is the maximum possible number of paths in an $$$i$$$-valid set of paths.
7
1 2
2 3
3 4
4 5
5 6
6 7
7
3
2
1
1
1
1
6
1 2
2 3
2 4
1 5
5 6
6
2
2
1
1
0
One way to achieve the optimal number of paths for the second sample is illustrated in the following picture:
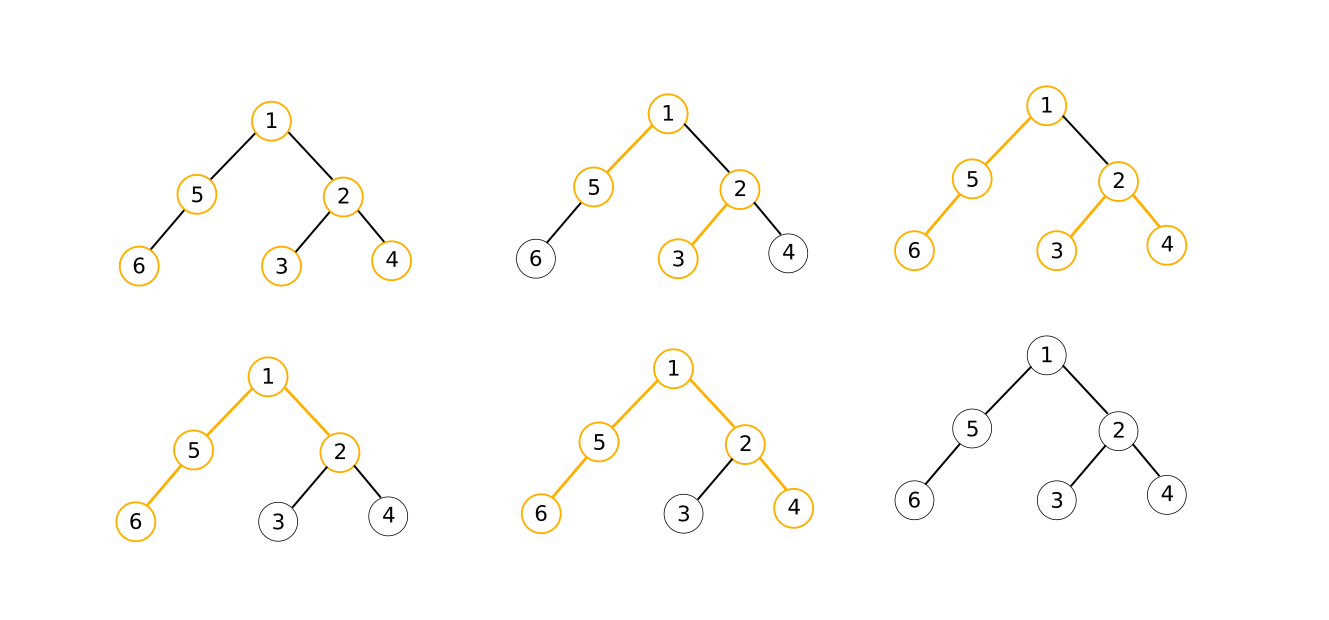
| Name |
|---|




