On a chessboard with a width of $$$10^9$$$ and a height of $$$10^9$$$, the rows are numbered from bottom to top from $$$1$$$ to $$$10^9$$$, and the columns are numbered from left to right from $$$1$$$ to $$$10^9$$$. Therefore, for each cell of the chessboard you can assign the coordinates $$$(x,y)$$$, where $$$x$$$ is the column number and $$$y$$$ is the row number.
Every day there are fights between black and white pieces on this board. Today, the black ones won, but at what price? Only the rook survived, and it was driven into the lower left corner — a cell with coordinates $$$(1,1)$$$. But it is still happy, because the victory has been won and it's time to celebrate it! In order to do this, the rook needs to go home, namely — on the upper side of the field (that is, in any cell that is in the row with number $$$10^9$$$).
Everything would have been fine, but the treacherous white figures put spells on some places of the field before the end of the game. There are two types of spells:
- Vertical. Each of these is defined by one number $$$x$$$. Such spells create an infinite blocking line between the columns $$$x$$$ and $$$x+1$$$.
- Horizontal. Each of these is defined by three numbers $$$x_1$$$, $$$x_2$$$, $$$y$$$. Such spells create a blocking segment that passes through the top side of the cells, which are in the row $$$y$$$ and in columns from $$$x_1$$$ to $$$x_2$$$ inclusive. The peculiarity of these spells is that it is impossible for a certain pair of such spells to have a common point. Note that horizontal spells can have common points with vertical spells.

Let's recall that the rook is a chess piece that in one move can move to any point that is in the same row or column with its initial position. In our task, the rook can move from the cell $$$(r_0,c_0)$$$ into the cell $$$(r_1,c_1)$$$ only under the condition that $$$r_1 = r_0$$$ or $$$c_1 = c_0$$$ and there is no blocking lines or blocking segments between these cells (For better understanding, look at the samples).
Fortunately, the rook can remove spells, but for this it has to put tremendous efforts, therefore, it wants to remove the minimum possible number of spells in such way, that after this it can return home. Find this number!
The first line contains two integers $$$n$$$ and $$$m$$$ ($$$0 \le n,m \le 10^5$$$) — the number of vertical and horizontal spells.
Each of the following $$$n$$$ lines contains one integer $$$x$$$ ($$$1 \le x < 10^9$$$) — the description of the vertical spell. It will create a blocking line between the columns of $$$x$$$ and $$$x+1$$$.
Each of the following $$$m$$$ lines contains three integers $$$x_1$$$, $$$x_2$$$ and $$$y$$$ ($$$1 \le x_{1} \le x_{2} \le 10^9$$$, $$$1 \le y < 10^9$$$) — the numbers that describe the horizontal spell. It will create a blocking segment that passes through the top sides of the cells that are in the row with the number $$$y$$$, in columns from $$$x_1$$$ to $$$x_2$$$ inclusive.
It is guaranteed that all spells are different, as well as the fact that for each pair of horizontal spells it is true that the segments that describe them do not have common points.
In a single line print one integer — the minimum number of spells the rook needs to remove so it can get from the cell $$$(1,1)$$$ to at least one cell in the row with the number $$$10^9$$$
2 3
6
8
1 5 6
1 9 4
2 4 2
1
1 3
4
1 5 3
1 9 4
4 6 6
1
0 2
1 1000000000 4
1 1000000000 2
2
0 0
0
2 3
4
6
1 4 3
1 5 2
1 6 5
2
In the first sample, in order for the rook return home, it is enough to remove the second horizontal spell.
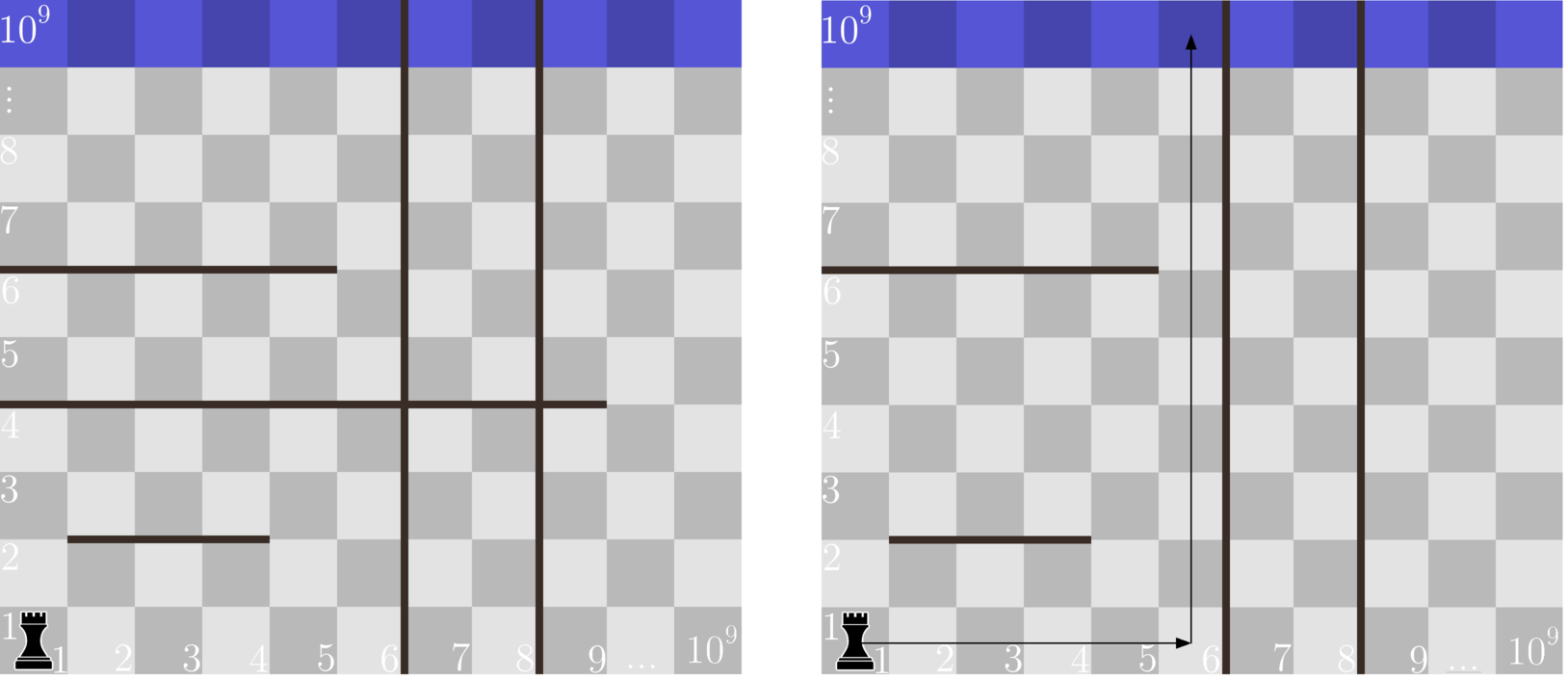 Illustration for the first sample. On the left it shows how the field looked at the beginning. On the right it shows how the field looked after the deletion of the second horizontal spell. It also shows the path, on which the rook would be going home.
Illustration for the first sample. On the left it shows how the field looked at the beginning. On the right it shows how the field looked after the deletion of the second horizontal spell. It also shows the path, on which the rook would be going home. In the second sample, in order for the rook to return home, it is enough to remove the only vertical spell. If we tried to remove just one of the horizontal spells, it would not allow the rook to get home, because it would be blocked from above by one of the remaining horizontal spells (either first one or second one), and to the right it would be blocked by a vertical spell.
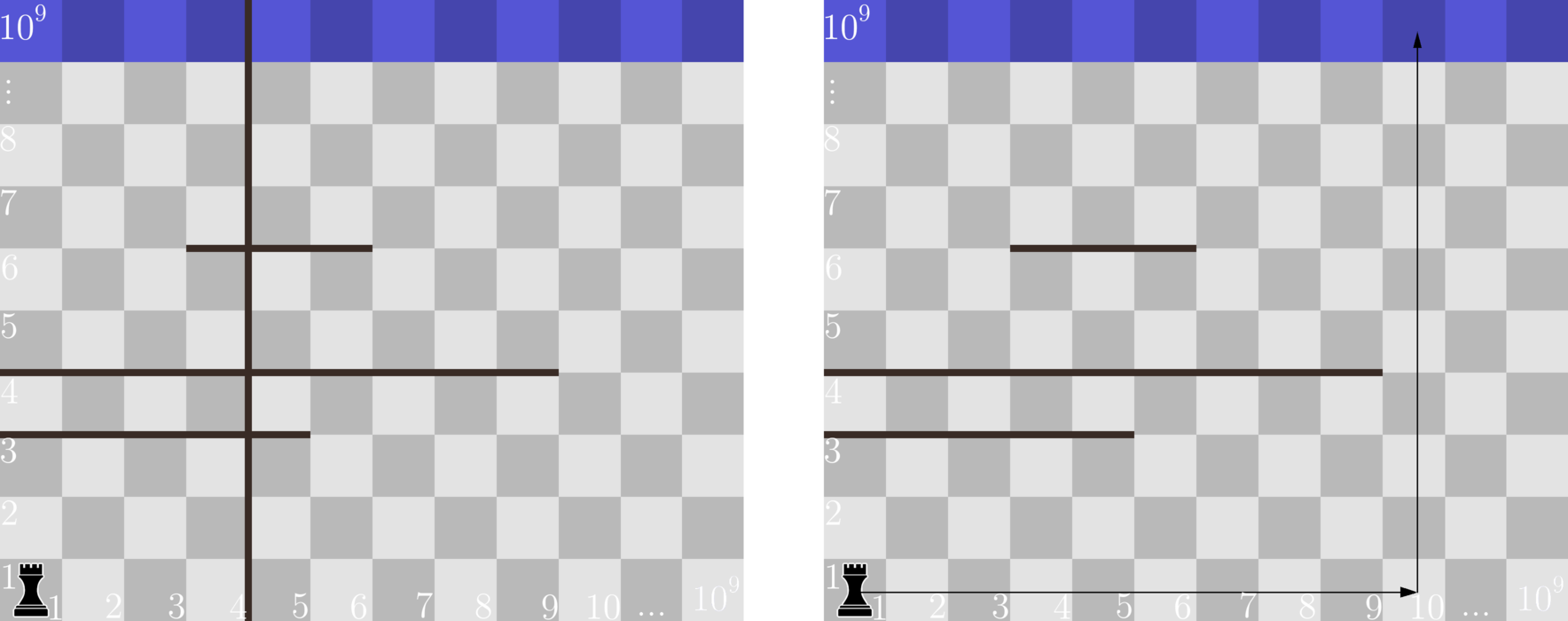 Illustration for the second sample. On the left it shows how the field looked at the beginning. On the right it shows how it looked after the deletion of the vertical spell. It also shows the path, on which the rook would be going home.
Illustration for the second sample. On the left it shows how the field looked at the beginning. On the right it shows how it looked after the deletion of the vertical spell. It also shows the path, on which the rook would be going home. In the third sample, we have two horizontal spells that go through the whole field. These spells can not be bypassed, so we need to remove both of them.
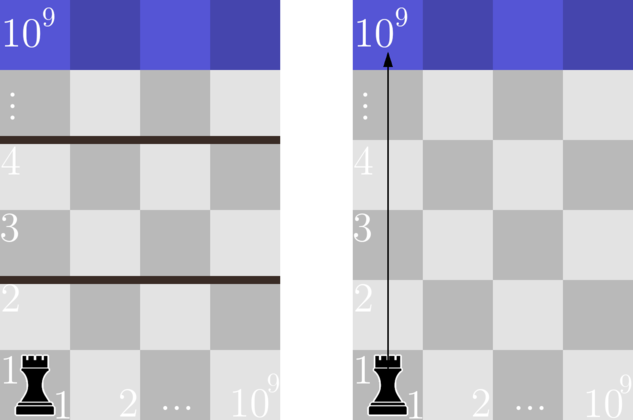 Illustration for the third sample. On the left it shows how the field looked at the beginning. On the right it shows how the field looked after the deletion of the horizontal spells. It also shows the path, on which the rook would be going home.
Illustration for the third sample. On the left it shows how the field looked at the beginning. On the right it shows how the field looked after the deletion of the horizontal spells. It also shows the path, on which the rook would be going home. In the fourth sample, we have no spells, which means that we do not need to remove anything.
In the fifth example, we can remove the first vertical and third horizontal spells.
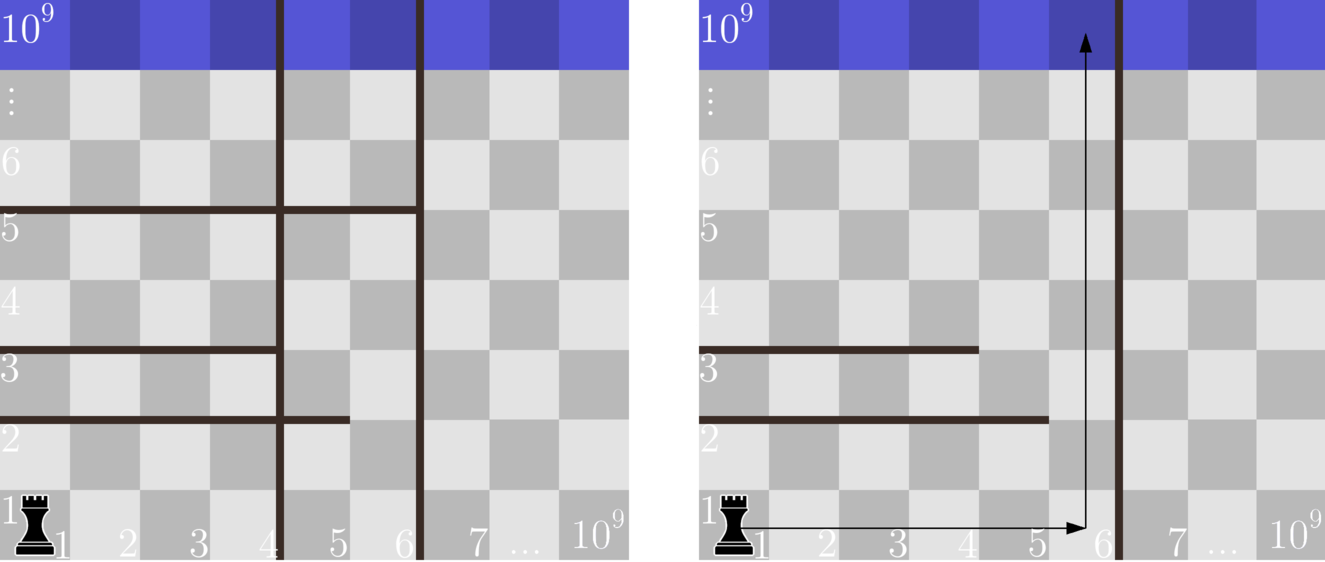 Illustration for the fifth sample. On the left it shows how the field looked at the beginning. On the right it shows how it looked after the deletions. It also shows the path, on which the rook would be going home.
Illustration for the fifth sample. On the left it shows how the field looked at the beginning. On the right it shows how it looked after the deletions. It also shows the path, on which the rook would be going home.
| Name |
|---|