You are given $$$n$$$ points on the plane. The polygon formed from all the $$$n$$$ points is strictly convex, that is, the polygon is convex, and there are no three collinear points (i.e. lying in the same straight line). The points are numbered from $$$1$$$ to $$$n$$$, in clockwise order.
We define the distance between two points $$$p_1 = (x_1, y_1)$$$ and $$$p_2 = (x_2, y_2)$$$ as their Manhattan distance: $$$$$$d(p_1, p_2) = |x_1 - x_2| + |y_1 - y_2|.$$$$$$
Furthermore, we define the perimeter of a polygon, as the sum of Manhattan distances between all adjacent pairs of points on it; if the points on the polygon are ordered as $$$p_1, p_2, \ldots, p_k$$$ $$$(k \geq 3)$$$, then the perimeter of the polygon is $$$d(p_1, p_2) + d(p_2, p_3) + \ldots + d(p_k, p_1)$$$.
For some parameter $$$k$$$, let's consider all the polygons that can be formed from the given set of points, having any $$$k$$$ vertices, such that the polygon is not self-intersecting. For each such polygon, let's consider its perimeter. Over all such perimeters, we define $$$f(k)$$$ to be the maximal perimeter.
Please note, when checking whether a polygon is self-intersecting, that the edges of a polygon are still drawn as straight lines. For instance, in the following pictures:
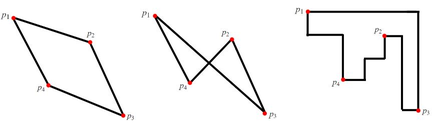
In the middle polygon, the order of points ($$$p_1, p_3, p_2, p_4$$$) is not valid, since it is a self-intersecting polygon. The right polygon (whose edges resemble the Manhattan distance) has the same order and is not self-intersecting, but we consider edges as straight lines. The correct way to draw this polygon is ($$$p_1, p_2, p_3, p_4$$$), which is the left polygon.
Your task is to compute $$$f(3), f(4), \ldots, f(n)$$$. In other words, find the maximum possible perimeter for each possible number of points (i.e. $$$3$$$ to $$$n$$$).
The first line contains a single integer $$$n$$$ ($$$3 \leq n \leq 3\cdot 10^5$$$) — the number of points.
Each of the next $$$n$$$ lines contains two integers $$$x_i$$$ and $$$y_i$$$ ($$$-10^8 \leq x_i, y_i \leq 10^8$$$) — the coordinates of point $$$p_i$$$.
The set of points is guaranteed to be convex, all points are distinct, the points are ordered in clockwise order, and there will be no three collinear points.
For each $$$i$$$ ($$$3\leq i\leq n$$$), output $$$f(i)$$$.
4
2 4
4 3
3 0
1 3
12 14
3
0 0
0 2
2 0
8
In the first example, for $$$f(3)$$$, we consider four possible polygons:
- ($$$p_1, p_2, p_3$$$), with perimeter $$$12$$$.
- ($$$p_1, p_2, p_4$$$), with perimeter $$$8$$$.
- ($$$p_1, p_3, p_4$$$), with perimeter $$$12$$$.
- ($$$p_2, p_3, p_4$$$), with perimeter $$$12$$$.
For $$$f(4)$$$, there is only one option, taking all the given points. Its perimeter $$$14$$$.
In the second example, there is only one possible polygon. Its perimeter is $$$8$$$.
| Name |
|---|