Есть $$$n$$$ точек на плоскости. Многоугольник, сформированный этими $$$n$$$ точками, строго выпуклый, то есть многоугольник выпуклый и нет трех коллинеарных точек (то есть лежащих на одной прямой). Точки пронумерованы от $$$1$$$ до $$$n$$$ по часовой стрелке.
Определим расстояние между двумя точками $$$p_1 = (x_1, y_1)$$$ и $$$p_2 = (x_2, y_2)$$$ как их манхэттенское расстояние: $$$$$$d(p_1, p_2) = |x_1 - x_2| + |y_1 - y_2|.$$$$$$
Более того, определим периметр многоугольника как сумму манхэттенских расстояний между всеми соседними парами точек на нем; если точки на многоугольнике упорядочены как $$$p_1, p_2, \ldots, p_k$$$ $$$(k \geq 3)$$$, тогда периметр многоугольника равен $$$d(p_1, p_2) + d(p_2, p_3) + \ldots + d(p_k, p_1)$$$.
Для некоторого параметра $$$k$$$ рассмотрим все многоугольники, которые могут быть сформированы из любых $$$k$$$ точек заданного многоугольникв и не самопересекаются. Для каждого такого многоугольника рассмотрим его периметр. Определим $$$f(k)$$$ как максимальный периметр среди всех таких многоугольников.
Обратите внимание, что при проверке многоугольника на самопересечение, ребра многоугольника рисуются как прямые линии. Например, на следующих рисунках:
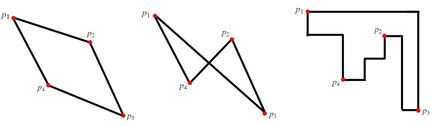
В многоугольнике, который изображен посередине, последовательность точек ($$$p_1, p_3, p_2, p_4$$$) неправильная потому, что многоугольник самопересекается. Правый многоугольник (ребра которого напоминают Манхэттенское расстояние) имеет такую же последовательность и не самопересекается, но мы рассматриваем ребра как прямые отрезки. Правильный способ нарисовать этот многоугольник — это использовать последовательность ($$$p_1, p_2, p_3, p_4$$$), пример которого можно увидеть на левом рисунке.
Вычислите $$$f(3), f(4), \ldots, f(n)$$$. Другими словами, найдите максимально возможный периметр для каждого количества точек (то есть от $$$3$$$ до $$$n$$$).
Первая строка содержит одно целое число $$$n$$$ ($$$3 \leq n \leq 3\cdot 10^5$$$) — количество точек.
Каждая из следующих $$$n$$$ строк содержит два целых числа $$$x_i$$$ и $$$y_i$$$ ($$$-10^8 \leq x_i, y_i \leq 10^8$$$) — координаты точки $$$p_i$$$.
Гарантируется, что множество точек выпуклое, все точки различны, они упорядочены по часовой стрелке, и нет трех коллинеарных точек.
Для каждого $$$i$$$ ($$$3\leq i\leq n$$$) выведите $$$f(i)$$$.
4
2 4
4 3
3 0
1 3
12 14
3
0 0
0 2
2 0
8
В первом примере для $$$f(3)$$$ есть четыре возможных многоугольника:
- ($$$p_1, p_2, p_3$$$) с периметром $$$12$$$.
- ($$$p_1, p_2, p_4$$$) с периметром $$$8$$$.
- ($$$p_1, p_3, p_4$$$) с периметром $$$12$$$.
- ($$$p_2, p_3, p_4$$$) с периметром $$$12$$$.
А для $$$f(4)$$$ есть всего один многоугольник, который состоит из всех точек. Его периметр $$$14$$$.
Во втором примере есть только один многоугольник, его периметр $$$8$$$.
| Название |
|---|