Let $$$T$$$ be a tree on $$$n$$$ vertices. Consider a graph $$$G_0$$$, initially equal to $$$T$$$. You are given a sequence of $$$q$$$ updates, where the $$$i$$$-th update is given as a pair of two distinct integers $$$u_i$$$ and $$$v_i$$$.
For every $$$i$$$ from $$$1$$$ to $$$q$$$, we define the graph $$$G_i$$$ as follows:
- If $$$G_{i-1}$$$ contains an edge $$$\{u_i, v_i\}$$$, then remove this edge to form $$$G_i$$$.
- Otherwise, add this edge to $$$G_{i-1}$$$ to form $$$G_i$$$.
Formally, $$$G_i := G_{i-1} \triangle \{\{u_i, v_i\}\}$$$ where $$$\triangle$$$ denotes the set symmetric difference.
Furthermore, it is guaranteed that $$$T$$$ is always a subgraph of $$$G_i$$$. In other words, an update never removes an edge of $$$T$$$.
Consider a connected graph $$$H$$$ and run a depth-first search on it. One can see that the tree edges (i.e. the edges leading to a not yet visited vertex at the time of traversal) form a spanning tree of the graph $$$H$$$. This spanning tree is not generally fixed for a particular graph — it depends on the starting vertex, and on the order in which the neighbors of each vertex are traversed.
We call vertex $$$w$$$ good if one can order the neighbors of each vertex in such a way that the depth-first search started from $$$w$$$ produces $$$T$$$ as the spanning tree. For every $$$i$$$ from $$$1$$$ to $$$q$$$, find and report the number of good vertices.
The first line contains two integers $$$n$$$ and $$$q$$$ ($$$3 \le n \le 2\cdot 10^5$$$, $$$1 \le q \le 2 \cdot 10^5$$$) — the number of nodes and the number of updates, respectively.
Each of the next $$$n-1$$$ lines contains two integers $$$u$$$ and $$$v$$$ ($$$1 \le u, v \le n$$$, $$$u \ne v$$$) — vertices connected by an edge in $$$T$$$. It is guaranteed that this graph is a tree.
Each of the next $$$q$$$ lines contains two integers $$$u$$$ and $$$v$$$ ($$$1 \le u, v \le n$$$, $$$u \ne v$$$) — the endpoints of the edge that is added or removed. It is guaranteed that this edge does not belong to $$$T$$$.
For each update, print one integer $$$k$$$ — the number of good vertices $$$w$$$ after the corresponding update.
3 2
1 2
1 3
2 3
3 2
2
3
6 6
1 2
2 3
1 4
4 5
1 6
2 5
3 4
5 2
6 4
3 4
6 5
3
2
3
2
3
2
The first sample is depicted in the following figure.
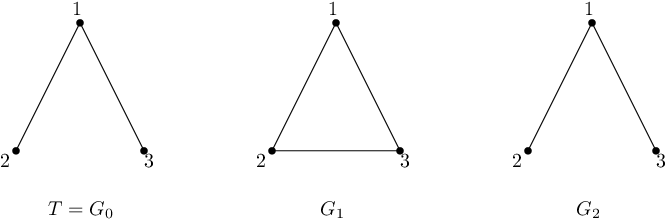
After the first update, $$$G$$$ contains all three possible edges. The result of a DFS is as follows:
- Let the starting vertex be $$$1$$$. We have two choices of ordering the neighbors of $$$1$$$, either $$$[2, 3]$$$ or $$$[3, 2]$$$.
- If we choose the former, then we reach vertex $$$2$$$. Regardless of the ordering of its neighbors, the next visited vertex will be $$$3$$$. Thus, the spanning tree generated by this DFS will contain edges $$$\{1, 2\}$$$ and $$$\{2, 3\}$$$, which does not equal to $$$T$$$.
- If we choose the latter, we obtain a spanning tree with edges $$$\{1, 3\}$$$ and $$$\{2, 3\}$$$.
- Let the starting vertex be $$$2$$$. We have two choices of traversing its neighbors. If we visit $$$3$$$ first, then the spanning tree will consist of edges $$$\{2,3\}$$$ and $$$\{1,3\}$$$, which is not equal to $$$T$$$. If we, however, visit $$$1$$$ first, then we can only continue to $$$3$$$ from here, and the spanning tree will consist of edges $$$\{1, 2\}$$$ and $$$\{1,3\}$$$, which equals to $$$T$$$. Hence, $$$2$$$ is a good vertex.
- The case when we start in the vertex $$$3$$$ is symmetrical to starting in $$$2$$$, and hence $$$3$$$ is a good vertex.
After the second update, the edge between $$$2$$$ and $$$3$$$ is removed, and $$$G = T$$$. It follows that the spanning tree generated by DFS will be always equal to $$$T$$$ independent of the choice of the starting vertex. Thus, the answer is $$$3$$$.
In the second sample, the set of good vertices after the corresponding query is:
- $$$\{2, 3, 5\}$$$
- $$$\{3, 5\}$$$
- $$$\{3, 4, 5\}$$$
- $$$\{4, 5\}$$$
- $$$\{4, 5, 6\}$$$
- $$$\{5, 6\}$$$
| Name |
|---|