Someone give a strange birthday present to Ivan. It is hedgehog — connected undirected graph in which one vertex has degree at least $$$3$$$ (we will call it center) and all other vertices has degree 1. Ivan thought that hedgehog is too boring and decided to make himself $$$k$$$-multihedgehog.
Let us define $$$k$$$-multihedgehog as follows:
- $$$1$$$-multihedgehog is hedgehog: it has one vertex of degree at least $$$3$$$ and some vertices of degree 1.
- For all $$$k \ge 2$$$, $$$k$$$-multihedgehog is $$$(k-1)$$$-multihedgehog in which the following changes has been made for each vertex $$$v$$$ with degree 1: let $$$u$$$ be its only neighbor; remove vertex $$$v$$$, create a new hedgehog with center at vertex $$$w$$$ and connect vertices $$$u$$$ and $$$w$$$ with an edge. New hedgehogs can differ from each other and the initial gift.
Thereby $$$k$$$-multihedgehog is a tree. Ivan made $$$k$$$-multihedgehog but he is not sure that he did not make any mistakes. That is why he asked you to check if his tree is indeed $$$k$$$-multihedgehog.
First line of input contains $$$2$$$ integers $$$n$$$, $$$k$$$ ($$$1 \le n \le 10^{5}$$$, $$$1 \le k \le 10^{9}$$$) — number of vertices and hedgehog parameter.
Next $$$n-1$$$ lines contains two integers $$$u$$$ $$$v$$$ ($$$1 \le u, \,\, v \le n; \,\, u \ne v$$$) — indices of vertices connected by edge.
It is guaranteed that given graph is a tree.
Print "Yes" (without quotes), if given graph is $$$k$$$-multihedgehog, and "No" (without quotes) otherwise.
14 2
1 4
2 4
3 4
4 13
10 5
11 5
12 5
14 5
5 13
6 7
8 6
13 6
9 6
Yes
3 1
1 3
2 3
No
2-multihedgehog from the first example looks like this:
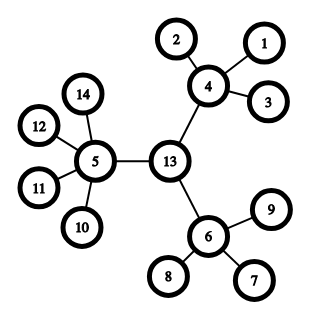
Its center is vertex $$$13$$$. Hedgehogs created on last step are: [4 (center), 1, 2, 3], [6 (center), 7, 8, 9], [5 (center), 10, 11, 12, 13].
Tree from second example is not a hedgehog because degree of center should be at least $$$3$$$.
| Name |
|---|




