| Technocup 2019 - Elimination Round 4 |
|---|
| Finished |
You are given a tree (an undirected connected graph without cycles) and an integer $$$s$$$.
Vanya wants to put weights on all edges of the tree so that all weights are non-negative real numbers and their sum is $$$s$$$. At the same time, he wants to make the diameter of the tree as small as possible.
Let's define the diameter of a weighed tree as the maximum sum of the weights of the edges lying on the path between two some vertices of the tree. In other words, the diameter of a weighed tree is the length of the longest simple path in the tree, where length of a path is equal to the sum of weights over all edges in the path.
Find the minimum possible diameter that Vanya can get.
The first line contains two integer numbers $$$n$$$ and $$$s$$$ ($$$2 \leq n \leq 10^5$$$, $$$1 \leq s \leq 10^9$$$) — the number of vertices in the tree and the sum of edge weights.
Each of the following $$$n−1$$$ lines contains two space-separated integer numbers $$$a_i$$$ and $$$b_i$$$ ($$$1 \leq a_i, b_i \leq n$$$, $$$a_i \neq b_i$$$) — the indexes of vertices connected by an edge. The edges are undirected.
It is guaranteed that the given edges form a tree.
Print the minimum diameter of the tree that Vanya can get by placing some non-negative real weights on its edges with the sum equal to $$$s$$$.
Your answer will be considered correct if its absolute or relative error does not exceed $$$10^{-6}$$$.
Formally, let your answer be $$$a$$$, and the jury's answer be $$$b$$$. Your answer is considered correct if $$$\frac {|a-b|} {max(1, b)} \leq 10^{-6}$$$.
4 3 1 2 1 3 1 4
2.000000000000000000
6 1 2 1 2 3 2 5 5 4 5 6
0.500000000000000000
5 5 1 2 2 3 3 4 3 5
3.333333333333333333
In the first example it is necessary to put weights like this:
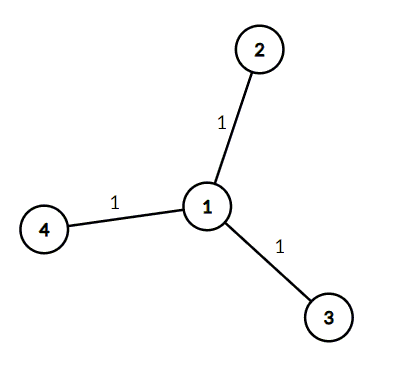
It is easy to see that the diameter of this tree is $$$2$$$. It can be proved that it is the minimum possible diameter.
In the second example it is necessary to put weights like this:
| Name |
|---|




