Petya loves lucky numbers. We all know that lucky numbers are the positive integers whose decimal representations contain only the lucky digits 4 and 7. For example, numbers 47, 744, 4 are lucky and 5, 17, 467 are not.
Petya and his friend Vasya play an interesting game. Petya randomly chooses an integer p from the interval [pl, pr] and Vasya chooses an integer v from the interval [vl, vr] (also randomly). Both players choose their integers equiprobably. Find the probability that the interval [min(v, p), max(v, p)] contains exactly k lucky numbers.
The single line contains five integers pl, pr, vl, vr and k (1 ≤ pl ≤ pr ≤ 109, 1 ≤ vl ≤ vr ≤ 109, 1 ≤ k ≤ 1000).
On the single line print the result with an absolute error of no more than 10 - 9.
1 10 1 10 2
0.320000000000
5 6 8 10 1
1.000000000000
Consider that [a, b] denotes an interval of integers; this interval includes the boundaries. That is, 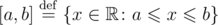
In first case there are 32 suitable pairs: (1, 7), (1, 8), (1, 9), (1, 10), (2, 7), (2, 8), (2, 9), (2, 10), (3, 7), (3, 8), (3, 9), (3, 10), (4, 7), (4, 8), (4, 9), (4, 10), (7, 1), (7, 2), (7, 3), (7, 4), (8, 1), (8, 2), (8, 3), (8, 4), (9, 1), (9, 2), (9, 3), (9, 4), (10, 1), (10, 2), (10, 3), (10, 4). Total number of possible pairs is 10·10 = 100, so answer is 32 / 100.
In second case Petya always get number less than Vasya and the only lucky 7 is between this numbers, so there will be always 1 lucky number.
| Name |
|---|




