| Codeforces Global Round 1 |
|---|
| Finished |
Let's define the Eulerian traversal of a tree (a connected undirected graph without cycles) as follows: consider a depth-first search algorithm which traverses vertices of the tree and enumerates them in the order of visiting (only the first visit of each vertex counts). This function starts from the vertex number $$$1$$$ and then recursively runs from all vertices which are connected with an edge with the current vertex and are not yet visited in increasing numbers order. Formally, you can describe this function using the following pseudocode:
next_id = 1
id = array of length n filled with -1
visited = array of length n filled with false
function dfs(v):
visited[v] = true
id[v] = next_id
next_id += 1
for to in neighbors of v in increasing order:
if not visited[to]:
dfs(to)
You are given a weighted tree, the vertices of which were enumerated with integers from $$$1$$$ to $$$n$$$ using the algorithm described above.
A leaf is a vertex of the tree which is connected with only one other vertex. In the tree given to you, the vertex $$$1$$$ is not a leaf. The distance between two vertices in the tree is the sum of weights of the edges on the simple path between them.
You have to answer $$$q$$$ queries of the following type: given integers $$$v$$$, $$$l$$$ and $$$r$$$, find the shortest distance from vertex $$$v$$$ to one of the leaves with indices from $$$l$$$ to $$$r$$$ inclusive.
The first line contains two integers $$$n$$$ and $$$q$$$ ($$$3 \leq n \leq 500\,000, 1 \leq q \leq 500\,000$$$) — the number of vertices in the tree and the number of queries, respectively.
The $$$(i - 1)$$$-th of the following $$$n - 1$$$ lines contains two integers $$$p_i$$$ and $$$w_i$$$ ($$$1 \leq p_i < i, 1 \leq w_i \leq 10^9$$$), denoting an edge between vertices $$$p_i$$$ and $$$i$$$ with the weight $$$w_i$$$.
It's guaranteed that the given edges form a tree and the vertices are enumerated in the Eulerian traversal order and that the vertex with index $$$1$$$ is not a leaf.
The next $$$q$$$ lines describe the queries. Each of them contains three integers $$$v_i$$$, $$$l_i$$$, $$$r_i$$$ ($$$1 \leq v_i \leq n, 1 \leq l_i \leq r_i \leq n$$$), describing the parameters of the query. It is guaranteed that there is at least one leaf with index $$$x$$$ such that $$$l_i \leq x \leq r_i$$$.
Output $$$q$$$ integers — the answers for the queries in the order they are given in the input.
5 3 1 10 1 1 3 2 3 3 1 1 5 5 4 5 4 1 2
3 0 13
5 3 1 1000000000 2 1000000000 1 1000000000 1 1000000000 3 4 5 2 1 5 2 4 5
3000000000 1000000000 2000000000
11 8 1 7 2 1 1 20 1 2 5 6 6 2 6 3 5 1 9 10 9 11 5 1 11 1 1 4 9 4 8 6 1 4 9 7 11 9 10 11 8 1 11 11 4 5
8 8 9 16 9 10 0 34
In the first example, the tree looks like this:
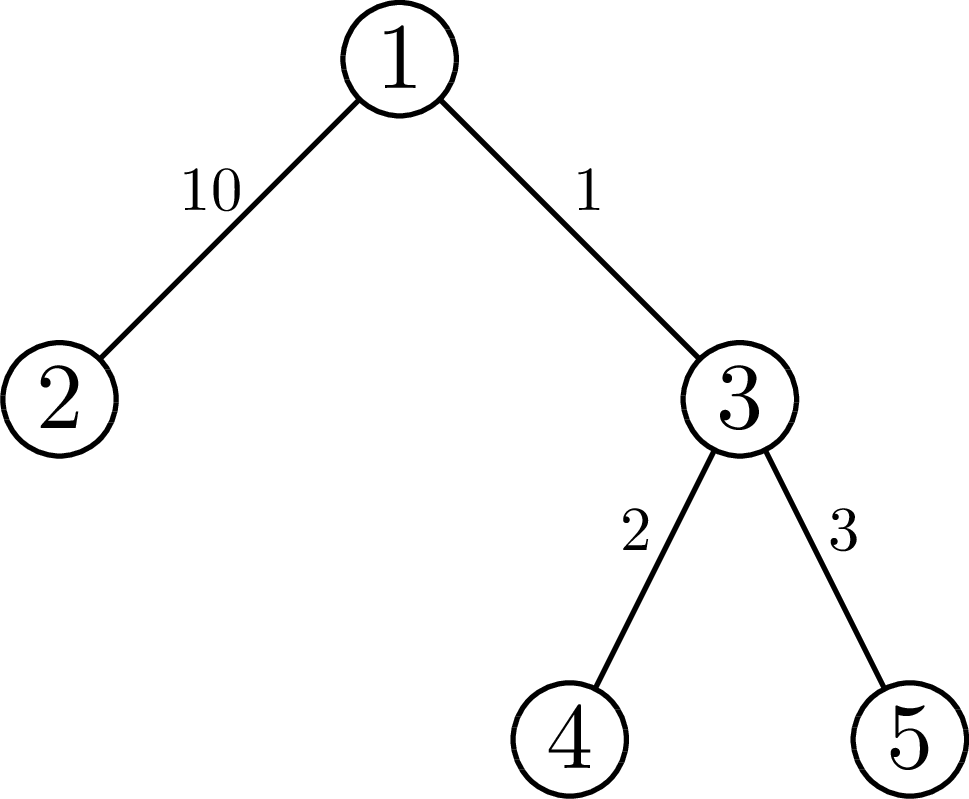
In the first query, the nearest leaf for the vertex $$$1$$$ is vertex $$$4$$$ with distance $$$3$$$. In the second query, the nearest leaf for vertex $$$5$$$ is vertex $$$5$$$ with distance $$$0$$$. In the third query the nearest leaf for vertex $$$4$$$ is vertex $$$4$$$; however, it is not inside interval $$$[1, 2]$$$ of the query. The only leaf in interval $$$[1, 2]$$$ is vertex $$$2$$$ with distance $$$13$$$ from vertex $$$4$$$.
| Name |
|---|




