| Codeforces Round 544 (Div. 3) |
|---|
| Finished |
You are given an undirected unweighted connected graph consisting of $$$n$$$ vertices and $$$m$$$ edges. It is guaranteed that there are no self-loops or multiple edges in the given graph.
Your task is to find any spanning tree of this graph such that the degree of the first vertex (vertex with label $$$1$$$ on it) is equal to $$$D$$$ (or say that there are no such spanning trees). Recall that the degree of a vertex is the number of edges incident to it.
The first line contains three integers $$$n$$$, $$$m$$$ and $$$D$$$ ($$$2 \le n \le 2 \cdot 10^5$$$, $$$n - 1 \le m \le min(2 \cdot 10^5, \frac{n(n-1)}{2}), 1 \le D < n$$$) — the number of vertices, the number of edges and required degree of the first vertex, respectively.
The following $$$m$$$ lines denote edges: edge $$$i$$$ is represented by a pair of integers $$$v_i$$$, $$$u_i$$$ ($$$1 \le v_i, u_i \le n$$$, $$$u_i \ne v_i$$$), which are the indices of vertices connected by the edge. There are no loops or multiple edges in the given graph, i. e. for each pair ($$$v_i, u_i$$$) there are no other pairs ($$$v_i, u_i$$$) or ($$$u_i, v_i$$$) in the list of edges, and for each pair $$$(v_i, u_i)$$$ the condition $$$v_i \ne u_i$$$ is satisfied.
If there is no spanning tree satisfying the condition from the problem statement, print "NO" in the first line.
Otherwise print "YES" in the first line and then print $$$n-1$$$ lines describing the edges of a spanning tree such that the degree of the first vertex (vertex with label $$$1$$$ on it) is equal to $$$D$$$. Make sure that the edges of the printed spanning tree form some subset of the input edges (order doesn't matter and edge $$$(v, u)$$$ is considered the same as the edge $$$(u, v)$$$).
If there are multiple possible answers, print any of them.
4 5 1 1 2 1 3 1 4 2 3 3 4
YES 2 1 2 3 3 4
4 5 3 1 2 1 3 1 4 2 3 3 4
YES 1 2 1 3 4 1
4 4 3 1 2 1 4 2 3 3 4
NO
The picture corresponding to the first and second examples: 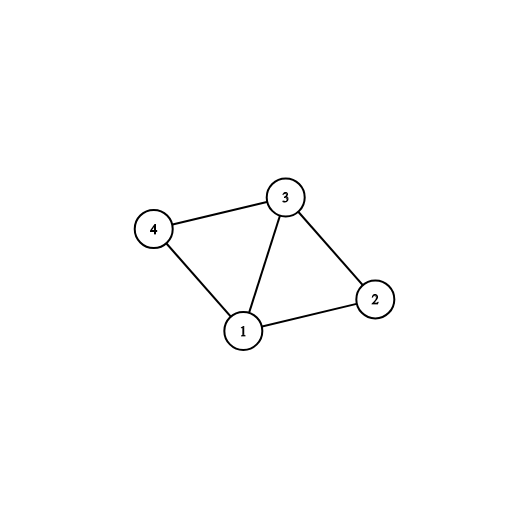
The picture corresponding to the third example: 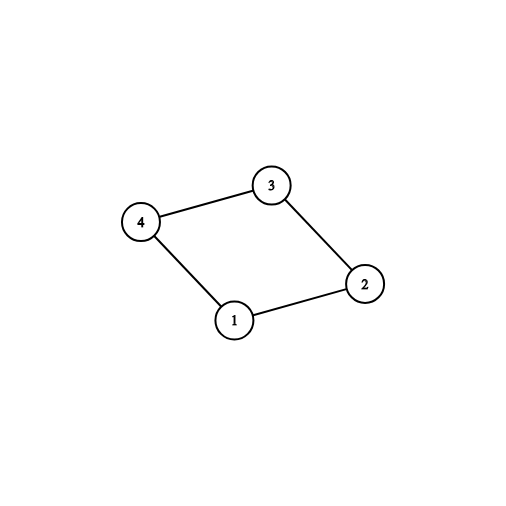
| Name |
|---|




