| Codeforces Beta Round 90 |
|---|
| Finished |
Vasya is about to take his first university exam in about several minutes. And it's not just some ordinary exam, it's on mathematical analysis. Of course, right now Vasya can only think of one thing: what the result of his talk with the examiner will be...
To prepare for the exam, one has to study proofs of n theorems. It is known that there will be k examination cards on the exam and each card contains 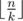 distinct theorems. Besides, no theorem is mentioned in more than one card (that is,
distinct theorems. Besides, no theorem is mentioned in more than one card (that is, 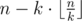 theorems won't be mentioned in any card). During the exam several students may get the same card.
theorems won't be mentioned in any card). During the exam several students may get the same card.
We do not know the exact way theorems are distributed by cards, however the students that took the exam before Vasya told him what theorems their cards contained. Vasya evaluates his level of proficiency in the i-th theorem by some number ai. The level of proficiency in some card is the average of the levels of proficiency in the theorems that are included in the card. Now Vasya wants to know the minimally and maximally possible levels of his proficiency in the card he gets on the exam. Vasya wants to determine it by the data he has collected from other students. Unfortunately, Vasya has no time left to do the math and he asked you to help him.
The first line contains two integers n and k (1 ≤ k ≤ n ≤ 100) — the number of theorems and the number of cards correspondingly. The second line contains n integers ai (0 ≤ ai ≤ 100), the i-th number (1 ≤ i ≤ n) corresponds to Vasya's proficiency in the i-th theorem.
The third line contains number q (0 ≤ q ≤ 100) — the number of people that have taken the exam before Vasya. Each of the following q lines contains the description of a student's card: 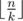 integers from 1 to n inclusive. They are the numbers of theorems included in the card in the order in which they are enumerated in the input data. The numbers are given in an arbitrary order. It is guaranteed that the given cards are valid (that is, that all theorems in one card are different and that different people get cards that either don't contain the same theorems or coincide up to the theorems' permutation).
integers from 1 to n inclusive. They are the numbers of theorems included in the card in the order in which they are enumerated in the input data. The numbers are given in an arbitrary order. It is guaranteed that the given cards are valid (that is, that all theorems in one card are different and that different people get cards that either don't contain the same theorems or coincide up to the theorems' permutation).
Print two real numbers, representing Vasya's minimum and maximum proficiency in the card he will get on the exam. The absolute or relative error should not exceed 10 - 6.
7 3
7 15 0 19 10 5 12
2
1 6
7 4
5.0000000000 15.5000000000
4 2
10 8 1 17
2
2 3
3 2
4.5000000000 13.5000000000
Let's analyze the first sample. Vasya's proficiency in the cards whose content he already knows equals 6 and 15.5 correspondingly. The three theorems that are left are only enough to make one exam card. If we consider all possible variants of theorems included in the card we can see that in the best case scenario Vasya gets the card that contains theorems 4 and 7 (his proficiency would equal 15.5) and in the worst case scenario he gets theorems 3 and 5 (his proficiency would equal 5).
The ⌊ x⌋ operation denotes taking integer part of real number x (rounding down).
| Name |
|---|




