| Codeforces Round 578 (Div. 2) |
|---|
| Finished |
Amugae is in a very large round corridor. The corridor consists of two areas. The inner area is equally divided by $$$n$$$ sectors, and the outer area is equally divided by $$$m$$$ sectors. A wall exists between each pair of sectors of same area (inner or outer), but there is no wall between the inner area and the outer area. A wall always exists at the 12 o'clock position.
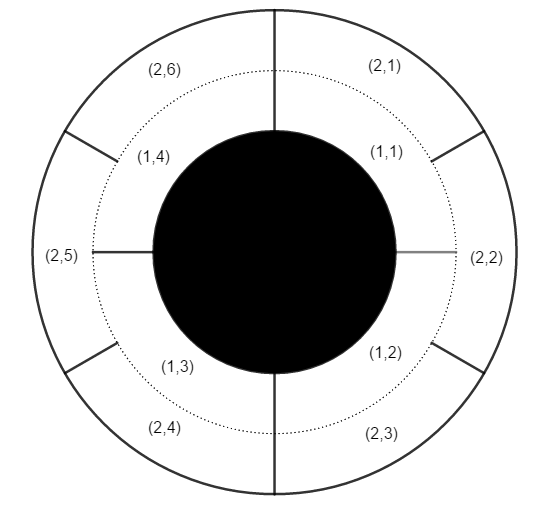
The inner area's sectors are denoted as $$$(1,1), (1,2), \dots, (1,n)$$$ in clockwise direction. The outer area's sectors are denoted as $$$(2,1), (2,2), \dots, (2,m)$$$ in the same manner. For a clear understanding, see the example image above.
Amugae wants to know if he can move from one sector to another sector. He has $$$q$$$ questions.
For each question, check if he can move between two given sectors.
The first line contains three integers $$$n$$$, $$$m$$$ and $$$q$$$ ($$$1 \le n, m \le 10^{18}$$$, $$$1 \le q \le 10^4$$$) — the number of sectors in the inner area, the number of sectors in the outer area and the number of questions.
Each of the next $$$q$$$ lines contains four integers $$$s_x$$$, $$$s_y$$$, $$$e_x$$$, $$$e_y$$$ ($$$1 \le s_x, e_x \le 2$$$; if $$$s_x = 1$$$, then $$$1 \le s_y \le n$$$, otherwise $$$1 \le s_y \le m$$$; constraints on $$$e_y$$$ are similar). Amague wants to know if it is possible to move from sector $$$(s_x, s_y)$$$ to sector $$$(e_x, e_y)$$$.
For each question, print "YES" if Amugae can move from $$$(s_x, s_y)$$$ to $$$(e_x, e_y)$$$, and "NO" otherwise.
You can print each letter in any case (upper or lower).
4 6 3 1 1 2 3 2 6 1 2 2 6 2 4
YES NO YES
Example is shown on the picture in the statement.
| Name |
|---|




