You have a string $$$s$$$ — a sequence of commands for your toy robot. The robot is placed in some cell of a rectangular grid. He can perform four commands:
- 'W' — move one cell up;
- 'S' — move one cell down;
- 'A' — move one cell left;
- 'D' — move one cell right.
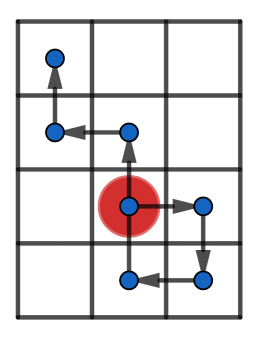
Let $$$Grid(s)$$$ be the grid of minimum possible area such that there is a position in the grid where you can place the robot in such a way that it will not fall from the grid while running the sequence of commands $$$s$$$. For example, if $$$s = \text{DSAWWAW}$$$ then $$$Grid(s)$$$ is the $$$4 \times 3$$$ grid:
- you can place the robot in the cell $$$(3, 2)$$$;
- the robot performs the command 'D' and moves to $$$(3, 3)$$$;
- the robot performs the command 'S' and moves to $$$(4, 3)$$$;
- the robot performs the command 'A' and moves to $$$(4, 2)$$$;
- the robot performs the command 'W' and moves to $$$(3, 2)$$$;
- the robot performs the command 'W' and moves to $$$(2, 2)$$$;
- the robot performs the command 'A' and moves to $$$(2, 1)$$$;
- the robot performs the command 'W' and moves to $$$(1, 1)$$$.
You have $$$4$$$ extra letters: one 'W', one 'A', one 'S', one 'D'. You'd like to insert at most one of these letters in any position of sequence $$$s$$$ to minimize the area of $$$Grid(s)$$$.
What is the minimum area of $$$Grid(s)$$$ you can achieve?
The first line contains one integer $$$T$$$ ($$$1 \le T \le 1000$$$) — the number of queries.
Next $$$T$$$ lines contain queries: one per line. This line contains single string $$$s$$$ ($$$1 \le |s| \le 2 \cdot 10^5$$$, $$$s_i \in \{\text{W}, \text{A}, \text{S}, \text{D}\}$$$) — the sequence of commands.
It's guaranteed that the total length of $$$s$$$ over all queries doesn't exceed $$$2 \cdot 10^5$$$.
Print $$$T$$$ integers: one per query. For each query print the minimum area of $$$Grid(s)$$$ you can achieve.
3 DSAWWAW D WA
8 2 4
In the first query you have to get string $$$\text{DSAWW}\underline{D}\text{AW}$$$.
In second and third queries you can not decrease the area of $$$Grid(s)$$$.
| Name |
|---|




