| Codeforces Round 582 (Div. 3) |
|---|
| Finished |
You are given a weighted tree consisting of $$$n$$$ vertices. Recall that a tree is a connected graph without cycles. Vertices $$$u_i$$$ and $$$v_i$$$ are connected by an edge with weight $$$w_i$$$.
You are given $$$m$$$ queries. The $$$i$$$-th query is given as an integer $$$q_i$$$. In this query you need to calculate the number of pairs of vertices $$$(u, v)$$$ ($$$u < v$$$) such that the maximum weight of an edge on a simple path between $$$u$$$ and $$$v$$$ doesn't exceed $$$q_i$$$.
The first line of the input contains two integers $$$n$$$ and $$$m$$$ ($$$1 \le n, m \le 2 \cdot 10^5$$$) — the number of vertices in the tree and the number of queries.
Each of the next $$$n - 1$$$ lines describes an edge of the tree. Edge $$$i$$$ is denoted by three integers $$$u_i$$$, $$$v_i$$$ and $$$w_i$$$ — the labels of vertices it connects ($$$1 \le u_i, v_i \le n$$$, $$$u_i \ne v_i$$$) and the weight of the edge ($$$1 \le w_i \le 2 \cdot 10^5$$$). It is guaranteed that the given edges form a tree.
The last line of the input contains $$$m$$$ integers $$$q_1, q_2, \dots, q_m$$$ ($$$1 \le q_i \le 2 \cdot 10^5$$$), where $$$q_i$$$ is the maximum weight of an edge in the $$$i$$$-th query.
Print $$$m$$$ integers — the answers to the queries. The $$$i$$$-th value should be equal to the number of pairs of vertices $$$(u, v)$$$ ($$$u < v$$$) such that the maximum weight of an edge on a simple path between $$$u$$$ and $$$v$$$ doesn't exceed $$$q_i$$$.
Queries are numbered from $$$1$$$ to $$$m$$$ in the order of the input.
7 5 1 2 1 3 2 3 2 4 1 4 5 2 5 7 4 3 6 2 5 2 3 4 1
21 7 15 21 3
1 2 1 2
0 0
3 3 1 2 1 2 3 2 1 3 2
1 3 3
The picture shows the tree from the first example: 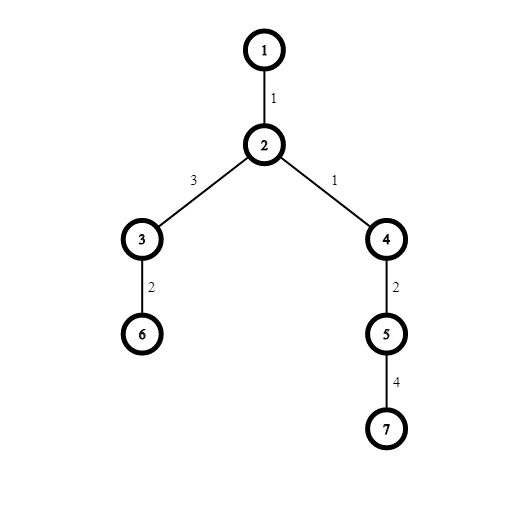
| Name |
|---|




