| Codeforces Round 589 (Div. 2) |
|---|
| Finished |
Suppose there is a $$$h \times w$$$ grid consisting of empty or full cells. Let's make some definitions:
- $$$r_{i}$$$ is the number of consecutive full cells connected to the left side in the $$$i$$$-th row ($$$1 \le i \le h$$$). In particular, $$$r_i=0$$$ if the leftmost cell of the $$$i$$$-th row is empty.
- $$$c_{j}$$$ is the number of consecutive full cells connected to the top end in the $$$j$$$-th column ($$$1 \le j \le w$$$). In particular, $$$c_j=0$$$ if the topmost cell of the $$$j$$$-th column is empty.
In other words, the $$$i$$$-th row starts exactly with $$$r_i$$$ full cells. Similarly, the $$$j$$$-th column starts exactly with $$$c_j$$$ full cells.
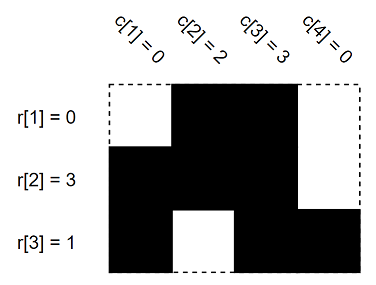 These are the $$$r$$$ and $$$c$$$ values of some $$$3 \times 4$$$ grid. Black cells are full and white cells are empty.
These are the $$$r$$$ and $$$c$$$ values of some $$$3 \times 4$$$ grid. Black cells are full and white cells are empty. You have values of $$$r$$$ and $$$c$$$. Initially, all cells are empty. Find the number of ways to fill grid cells to satisfy values of $$$r$$$ and $$$c$$$. Since the answer can be very large, find the answer modulo $$$1000000007\,(10^{9} + 7)$$$. In other words, find the remainder after division of the answer by $$$1000000007\,(10^{9} + 7)$$$.
The first line contains two integers $$$h$$$ and $$$w$$$ ($$$1 \le h, w \le 10^{3}$$$) — the height and width of the grid.
The second line contains $$$h$$$ integers $$$r_{1}, r_{2}, \ldots, r_{h}$$$ ($$$0 \le r_{i} \le w$$$) — the values of $$$r$$$.
The third line contains $$$w$$$ integers $$$c_{1}, c_{2}, \ldots, c_{w}$$$ ($$$0 \le c_{j} \le h$$$) — the values of $$$c$$$.
Print the answer modulo $$$1000000007\,(10^{9} + 7)$$$.
3 4 0 3 1 0 2 3 0
2
1 1 0 1
0
19 16 16 16 16 16 15 15 0 5 0 4 9 9 1 4 4 0 8 16 12 6 12 19 15 8 6 19 19 14 6 9 16 10 11 15 4
797922655
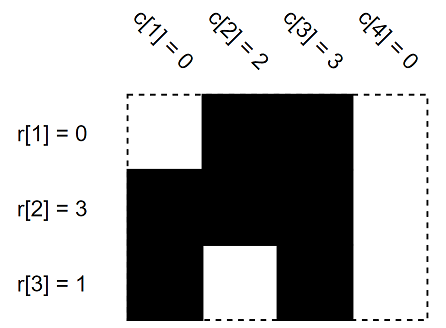
In the first example, this is the other possible case.
In the second example, it's impossible to make a grid to satisfy such $$$r$$$, $$$c$$$ values.
In the third example, make sure to print answer modulo $$$(10^9 + 7)$$$.
| Name |
|---|




