Pathfinding is a task of finding a route between two points. It often appears in many problems. For example, in a GPS navigation software where a driver can query for a suggested route, or in a robot motion planning where it should find a valid sequence of movements to do some tasks, or in a simple maze solver where it should find a valid path from one point to another point. This problem is related to solving a maze.
The maze considered in this problem is in the form of a matrix of integers $$$A$$$ of $$$N \times N$$$. The value of each cell is generated from a given array $$$R$$$ and $$$C$$$ of $$$N$$$ integers each. Specifically, the value on the $$$i^{th}$$$ row and $$$j^{th}$$$ column, cell $$$(i,j)$$$, is equal to $$$R_i + C_j$$$. Note that all indexes in this problem are from $$$1$$$ to $$$N$$$.
A path in this maze is defined as a sequence of cells $$$(r_1,c_1), (r_2,c_2), \dots, (r_k,c_k)$$$ such that $$$|r_i - r_{i+1}| + |c_i - c_{i+1}| = 1$$$ for all $$$1 \le i < k$$$. In other words, each adjacent cell differs only by $$$1$$$ row or only by $$$1$$$ column. An even path in this maze is defined as a path in which all the cells in the path contain only even numbers.
Given a tuple $$$\langle r_a,c_a,r_b,c_b \rangle$$$ as a query, your task is to determine whether there exists an even path from cell $$$(r_a,c_a)$$$ to cell $$$(r_b,c_b)$$$. To simplify the problem, it is guaranteed that both cell $$$(r_a,c_a)$$$ and cell $$$(r_b,c_b)$$$ contain even numbers.
For example, let $$$N = 5$$$, $$$R = \{6, 2, 7, 8, 3\}$$$, and $$$C = \{3, 4, 8, 5, 1\}$$$. The following figure depicts the matrix $$$A$$$ of $$$5 \times 5$$$ which is generated from the given array $$$R$$$ and $$$C$$$.
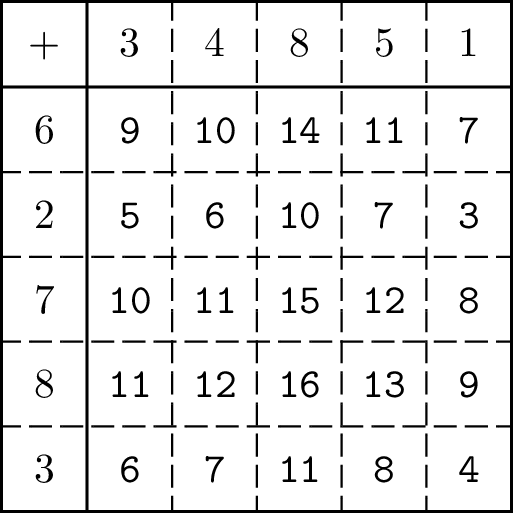
Let us consider several queries:
- $$$\langle 2, 2, 1, 3 \rangle$$$: There is an even path from cell $$$(2,2)$$$ to cell $$$(1,3)$$$, e.g., $$$(2,2), (2,3), (1,3)$$$. Of course, $$$(2,2), (1,2), (1,3)$$$ is also a valid even path.
- $$$\langle 4, 2, 4, 3 \rangle$$$: There is an even path from cell $$$(4,2)$$$ to cell $$$(4,3)$$$, namely $$$(4,2), (4,3)$$$.
- $$$\langle 5, 1, 3, 4 \rangle$$$: There is no even path from cell $$$(5,1)$$$ to cell $$$(3,4)$$$. Observe that the only two neighboring cells of $$$(5,1)$$$ are cell $$$(5,2)$$$ and cell $$$(4,1)$$$, and both of them contain odd numbers (7 and 11, respectively), thus, there cannot be any even path originating from cell $$$(5,1)$$$.
Input begins with a line containing two integers: $$$N$$$ $$$Q$$$ ($$$2 \le N \le 100\,000$$$; $$$1 \le Q \le 100\,000$$$) representing the size of the maze and the number of queries, respectively. The next line contains $$$N$$$ integers: $$$R_i$$$ ($$$0 \le R_i \le 10^6$$$) representing the array $$$R$$$. The next line contains $$$N$$$ integers: $$$C_i$$$ ($$$0 \le C_i \le 10^6$$$) representing the array $$$C$$$. The next $$$Q$$$ lines each contains four integers: $$$r_a$$$ $$$c_a$$$ $$$r_b$$$ $$$c_b$$$ ($$$1 \le r_a, c_a, r_b, c_b \le N$$$) representing a query of $$$\langle r_a, c_a, r_b, c_b \rangle$$$. It is guaranteed that $$$(r_a,c_a)$$$ and $$$(r_b,c_b)$$$ are two different cells in the maze and both of them contain even numbers.
For each query in the same order as input, output in a line a string "YES" (without quotes) or "NO" (without quotes) whether there exists an even path from cell $$$(r_a,c_a)$$$ to cell $$$(r_b,c_b)$$$.
5 3 6 2 7 8 3 3 4 8 5 1 2 2 1 3 4 2 4 3 5 1 3 4
YES YES NO
3 2 30 40 49 15 20 25 2 2 3 3 1 2 2 2
NO YES
Explanation for the sample input/output #1
This is the example from the problem description.
| Name |
|---|




