| Codeforces Round 630 (Div. 2) |
|---|
| Finished |
Eric is the teacher of graph theory class. Today, Eric teaches independent set and edge-induced subgraph.
Given a graph $$$G=(V,E)$$$, an independent set is a subset of vertices $$$V' \subset V$$$ such that for every pair $$$u,v \in V'$$$, $$$(u,v) \not \in E$$$ (i.e. no edge in $$$E$$$ connects two vertices from $$$V'$$$).
An edge-induced subgraph consists of a subset of edges $$$E' \subset E$$$ and all the vertices in the original graph that are incident on at least one edge in the subgraph.
Given $$$E' \subset E$$$, denote $$$G[E']$$$ the edge-induced subgraph such that $$$E'$$$ is the edge set of the subgraph. Here is an illustration of those definitions:
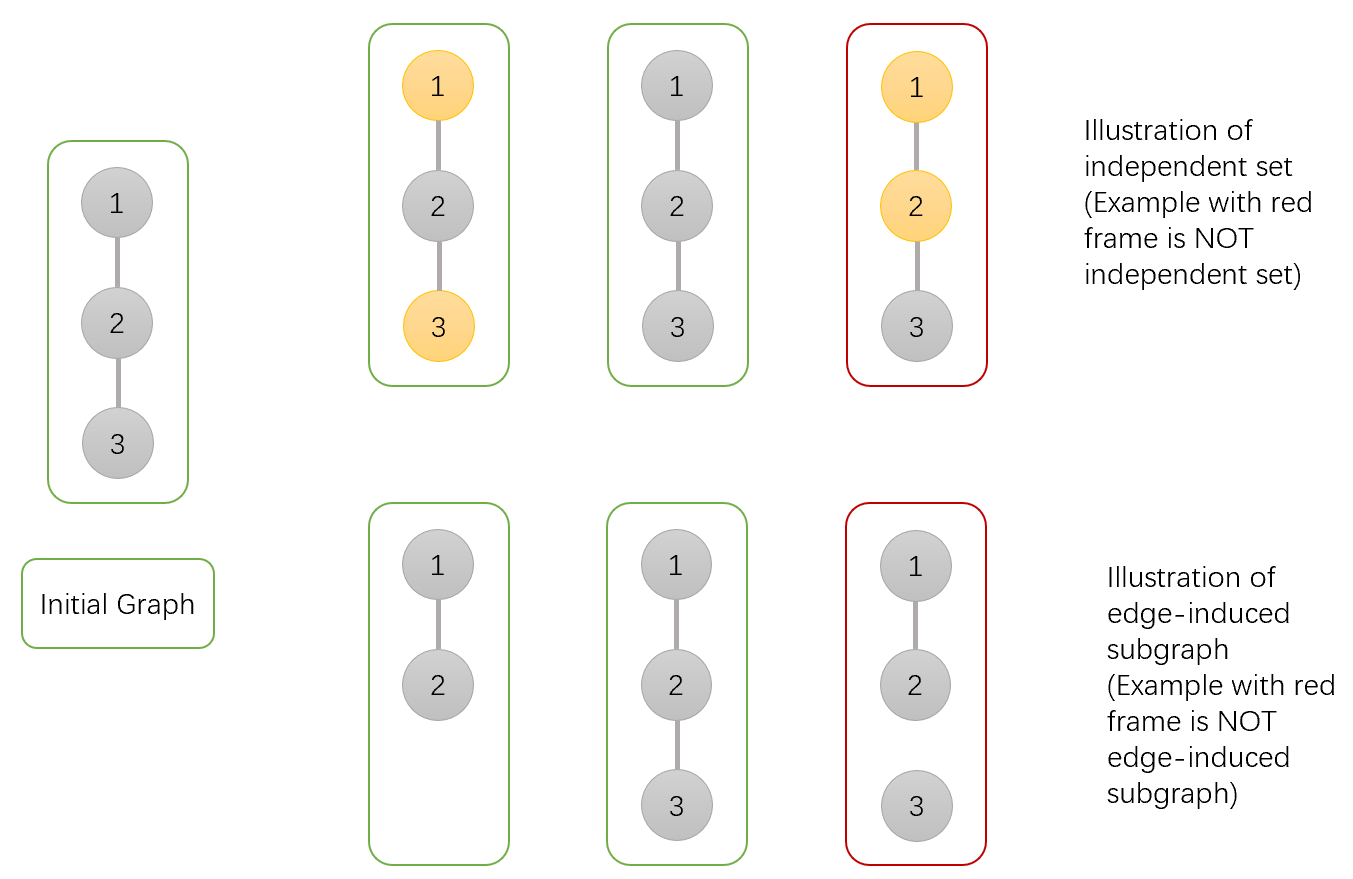
In order to help his students get familiar with those definitions, he leaves the following problem as an exercise:
Given a tree $$$G=(V,E)$$$, calculate the sum of $$$w(H)$$$ over all except null edge-induced subgraph $$$H$$$ of $$$G$$$, where $$$w(H)$$$ is the number of independent sets in $$$H$$$. Formally, calculate $$$\sum \limits_{\emptyset \not= E' \subset E} w(G[E'])$$$.
Show Eric that you are smarter than his students by providing the correct answer as quickly as possible. Note that the answer might be large, you should output the answer modulo $$$998,244,353$$$.
The first line contains a single integer $$$n$$$ ($$$2 \le n \le 3 \cdot 10^5$$$), representing the number of vertices of the graph $$$G$$$.
Each of the following $$$n-1$$$ lines contains two integers $$$u$$$ and $$$v$$$ ($$$1 \le u,v \le n$$$, $$$u \not= v$$$), describing edges of the given tree.
It is guaranteed that the given edges form a tree.
Output one integer, representing the desired value modulo $$$998,244,353$$$.
2 2 1
3
3 1 2 3 2
11
For the second example, all independent sets are listed below.
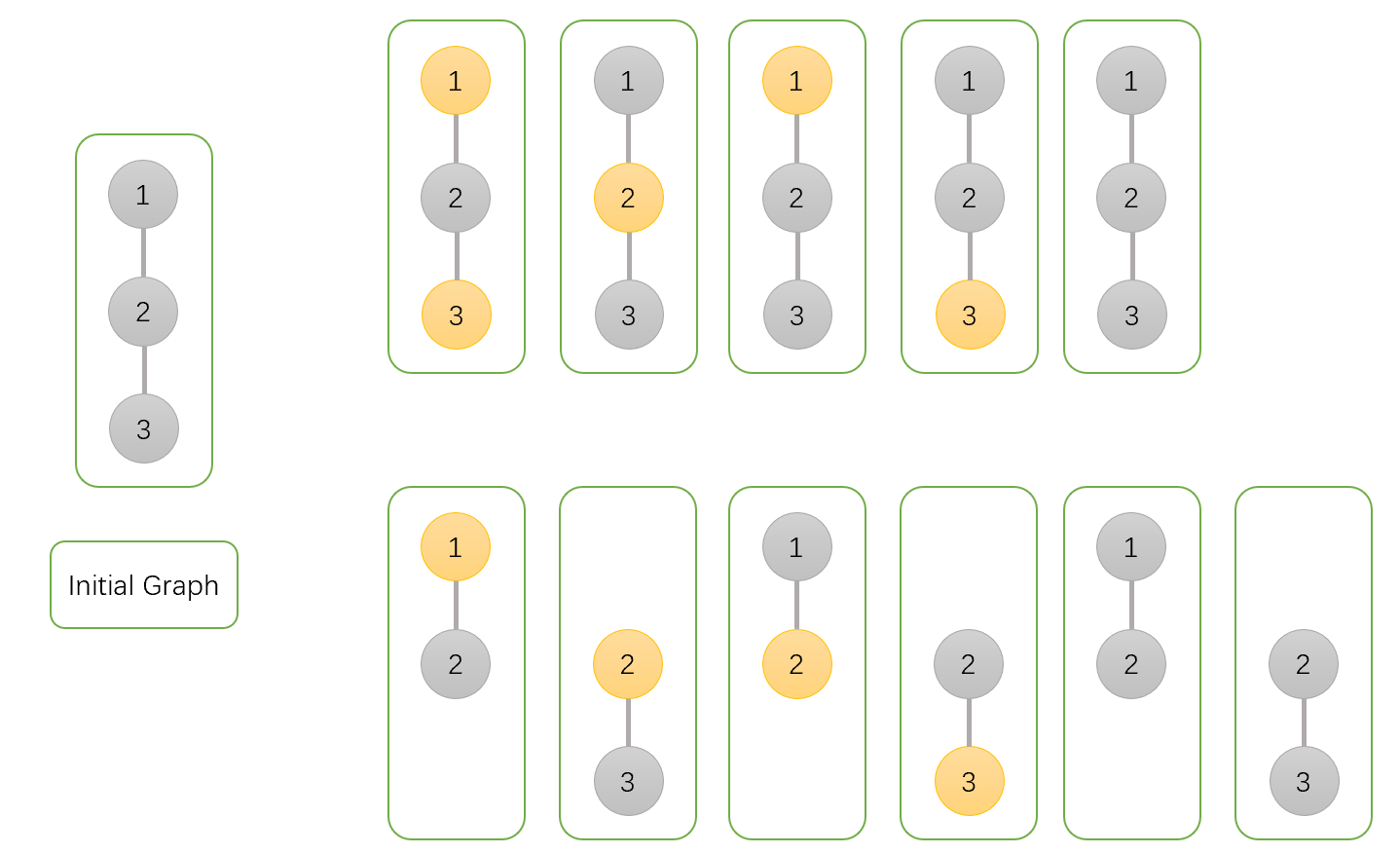
| Name |
|---|




