| Codeforces Round 665 (Div. 2) |
|---|
| Finished |
You are given a tree that consists of $$$n$$$ nodes. You should label each of its $$$n-1$$$ edges with an integer in such way that satisfies the following conditions:
- each integer must be greater than $$$0$$$;
- the product of all $$$n-1$$$ numbers should be equal to $$$k$$$;
- the number of $$$1$$$-s among all $$$n-1$$$ integers must be minimum possible.
Let's define $$$f(u,v)$$$ as the sum of the numbers on the simple path from node $$$u$$$ to node $$$v$$$. Also, let $$$\sum\limits_{i=1}^{n-1} \sum\limits_{j=i+1}^n f(i,j)$$$ be a distribution index of the tree.
Find the maximum possible distribution index you can get. Since answer can be too large, print it modulo $$$10^9 + 7$$$.
In this problem, since the number $$$k$$$ can be large, the result of the prime factorization of $$$k$$$ is given instead.
The first line contains one integer $$$t$$$ ($$$1 \le t \le 100$$$) — the number of test cases.
The first line of each test case contains a single integer $$$n$$$ ($$$2 \le n \le 10^5$$$) — the number of nodes in the tree.
Each of the next $$$n-1$$$ lines describes an edge: the $$$i$$$-th line contains two integers $$$u_i$$$ and $$$v_i$$$ ($$$1 \le u_i, v_i \le n$$$; $$$u_i \ne v_i$$$) — indices of vertices connected by the $$$i$$$-th edge.
Next line contains a single integer $$$m$$$ ($$$1 \le m \le 6 \cdot 10^4$$$) — the number of prime factors of $$$k$$$.
Next line contains $$$m$$$ prime numbers $$$p_1, p_2, \ldots, p_m$$$ ($$$2 \le p_i < 6 \cdot 10^4$$$) such that $$$k = p_1 \cdot p_2 \cdot \ldots \cdot p_m$$$.
It is guaranteed that the sum of $$$n$$$ over all test cases doesn't exceed $$$10^5$$$, the sum of $$$m$$$ over all test cases doesn't exceed $$$6 \cdot 10^4$$$, and the given edges for each test cases form a tree.
Print the maximum distribution index you can get. Since answer can be too large, print it modulo $$$10^9+7$$$.
3 4 1 2 2 3 3 4 2 2 2 4 3 4 1 3 3 2 2 3 2 7 6 1 2 3 4 6 7 3 5 1 3 6 4 7 5 13 3
17 18 286
In the first test case, one of the optimal ways is on the following image:

In this case, $$$f(1,2)=1$$$, $$$f(1,3)=3$$$, $$$f(1,4)=5$$$, $$$f(2,3)=2$$$, $$$f(2,4)=4$$$, $$$f(3,4)=2$$$, so the sum of these $$$6$$$ numbers is $$$17$$$.
In the second test case, one of the optimal ways is on the following image:
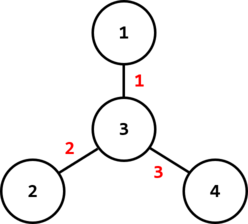
In this case, $$$f(1,2)=3$$$, $$$f(1,3)=1$$$, $$$f(1,4)=4$$$, $$$f(2,3)=2$$$, $$$f(2,4)=5$$$, $$$f(3,4)=3$$$, so the sum of these $$$6$$$ numbers is $$$18$$$.
| Name |
|---|




