| Codeforces Round 125 (Div. 1) |
|---|
| Finished |
Qwerty the Ranger arrived to the Diatar system with a very important task. He should deliver a special carcinogen for scientific research to planet Persephone. This is urgent, so Qwerty has to get to the planet as soon as possible. A lost day may fail negotiations as nobody is going to pay for an overdue carcinogen.
You can consider Qwerty's ship, the planet Persephone and the star Diatar points on a plane. Diatar is located in the origin of coordinate axes — at point (0, 0). Persephone goes round Diatar along a circular orbit with radius R in the counter-clockwise direction at constant linear speed vp (thus, for instance, a full circle around the star takes 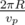 of time). At the initial moment of time Persephone is located at point (xp, yp).
of time). At the initial moment of time Persephone is located at point (xp, yp).
At the initial moment of time Qwerty's ship is at point (x, y). Qwerty can move in any direction at speed of at most v (v > vp). The star Diatar is hot (as all stars), so Qwerty can't get too close to it. The ship's metal sheathing melts at distance r (r < R) from the star.
Find the minimum time Qwerty needs to get the carcinogen to planet Persephone.
The first line contains space-separated integers xp, yp and vp ( - 104 ≤ xp, yp ≤ 104, 1 ≤ vp < 104) — Persephone's initial position and the speed at which it goes round Diatar.
The second line contains space-separated integers x, y, v and r ( - 104 ≤ x, y ≤ 104, 1 < v ≤ 104, 1 ≤ r ≤ 104) — The intial position of Qwerty's ship, its maximum speed and the minimum safe distance to star Diatar.
It is guaranteed that r2 < x2 + y2, r2 < xp2 + yp2 and vp < v.
Print a single real number — the minimum possible delivery time. The answer will be considered valid if its absolute or relative error does not exceed 10 - 6.
10 0 1
-10 0 2 8
9.584544103
50 60 10
50 60 20 40
0.000000000
| Name |
|---|




