| Codeforces Round 132 (Div. 2) |
|---|
| Finished |
Vasya's bicycle chain drive consists of two parts: n stars are attached to the pedal axle, m stars are attached to the rear wheel axle. The chain helps to rotate the rear wheel by transmitting the pedal rotation.
We know that the i-th star on the pedal axle has ai (0 < a1 < a2 < ... < an) teeth, and the j-th star on the rear wheel axle has bj (0 < b1 < b2 < ... < bm) teeth. Any pair (i, j) (1 ≤ i ≤ n; 1 ≤ j ≤ m) is called a gear and sets the indexes of stars to which the chain is currently attached. Gear (i, j) has a gear ratio, equal to the value 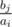 .
.
Since Vasya likes integers, he wants to find such gears (i, j), that their ratios are integers. On the other hand, Vasya likes fast driving, so among all "integer" gears (i, j) he wants to choose a gear with the maximum ratio. Help him to find the number of such gears.
In the problem, fraction 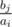 denotes division in real numbers, that is, no rounding is performed.
denotes division in real numbers, that is, no rounding is performed.
The first input line contains integer n (1 ≤ n ≤ 50) — the number of stars on the bicycle's pedal axle. The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 104) in the order of strict increasing.
The third input line contains integer m (1 ≤ m ≤ 50) — the number of stars on the rear wheel axle. The fourth line contains m integers b1, b2, ..., bm (1 ≤ bi ≤ 104) in the order of strict increasing.
It is guaranteed that there exists at least one gear (i, j), that its gear ratio is an integer. The numbers on the lines are separated by spaces.
Print the number of "integer" gears with the maximum ratio among all "integer" gears.
2
4 5
3
12 13 15
2
4
1 2 3 4
5
10 11 12 13 14
1
In the first sample the maximum "integer" gear ratio equals 3. There are two gears that have such gear ratio. For one of them a1 = 4, b1 = 12, and for the other a2 = 5, b3 = 15.
| Name |
|---|




