| Codeforces Round 172 (Div. 1) |
|---|
| Finished |
Bike loves looking for the second maximum element in the sequence. The second maximum element in the sequence of distinct numbers x1, x2, ..., xk (k > 1) is such maximum element xj, that the following inequality holds: 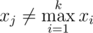 .
.
The lucky number of the sequence of distinct positive integers x1, x2, ..., xk (k > 1) is the number that is equal to the bitwise excluding OR of the maximum element of the sequence and the second maximum element of the sequence.
You've got a sequence of distinct positive integers s1, s2, ..., sn (n > 1). Let's denote sequence sl, sl + 1, ..., sr as s[l..r] (1 ≤ l < r ≤ n). Your task is to find the maximum number among all lucky numbers of sequences s[l..r].
Note that as all numbers in sequence s are distinct, all the given definitions make sence.
The first line contains integer n (1 < n ≤ 105). The second line contains n distinct integers s1, s2, ..., sn (1 ≤ si ≤ 109).
Print a single integer — the maximum lucky number among all lucky numbers of sequences s[l..r].
5
5 2 1 4 3
7
5
9 8 3 5 7
15
For the first sample you can choose s[4..5] = {4, 3} and its lucky number is (4 xor 3) = 7. You can also choose s[1..2].
For the second sample you must choose s[2..5] = {8, 3, 5, 7}.
| Name |
|---|




