| Codeforces Round 209 (Div. 2) |
|---|
| Finished |
Simon has a prime number x and an array of non-negative integers a1, a2, ..., an.
Simon loves fractions very much. Today he wrote out number  on a piece of paper. After Simon led all fractions to a common denominator and summed them up, he got a fraction:
on a piece of paper. After Simon led all fractions to a common denominator and summed them up, he got a fraction:  , where number t equals xa1 + a2 + ... + an. Now Simon wants to reduce the resulting fraction.
, where number t equals xa1 + a2 + ... + an. Now Simon wants to reduce the resulting fraction.
Help him, find the greatest common divisor of numbers s and t. As GCD can be rather large, print it as a remainder after dividing it by number 1000000007 (109 + 7).
The first line contains two positive integers n and x (1 ≤ n ≤ 105, 2 ≤ x ≤ 109) — the size of the array and the prime number.
The second line contains n space-separated integers a1, a2, ..., an (0 ≤ a1 ≤ a2 ≤ ... ≤ an ≤ 109).
Print a single number — the answer to the problem modulo 1000000007 (109 + 7).
2 2
2 2
8
3 3
1 2 3
27
2 2
29 29
73741817
4 5
0 0 0 0
1
In the first sample 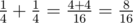 . Thus, the answer to the problem is 8.
. Thus, the answer to the problem is 8.
In the second sample, 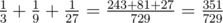 . The answer to the problem is 27, as 351 = 13·27, 729 = 27·27.
. The answer to the problem is 27, as 351 = 13·27, 729 = 27·27.
In the third sample the answer to the problem is 1073741824 mod 1000000007 = 73741817.
In the fourth sample 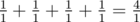 . Thus, the answer to the problem is 1.
. Thus, the answer to the problem is 1.
| Name |
|---|




