| Codeforces Round 223 (Div. 1) |
|---|
| Finished |
Sereja adores trees. Today he came up with a revolutionary new type of binary root trees.
His new tree consists of n levels, each vertex is indexed by two integers: the number of the level and the number of the vertex on the current level. The tree root is at level 1, its index is (1, 1). Here is a pseudo code of tree construction.
//the global data are integer arrays cnt[], left[][], right[][]
cnt[1] = 1;
fill arrays left[][], right[][] with values -1;
for(level = 1; level < n; level = level + 1){
cnt[level + 1] = 0;
for(position = 1; position <= cnt[level]; position = position + 1){
if(the value of position is a power of two){ // that is, 1, 2, 4, 8...
left[level][position] = cnt[level + 1] + 1;
right[level][position] = cnt[level + 1] + 2;
cnt[level + 1] = cnt[level + 1] + 2;
}else{
right[level][position] = cnt[level + 1] + 1;
cnt[level + 1] = cnt[level + 1] + 1;
}
}
}
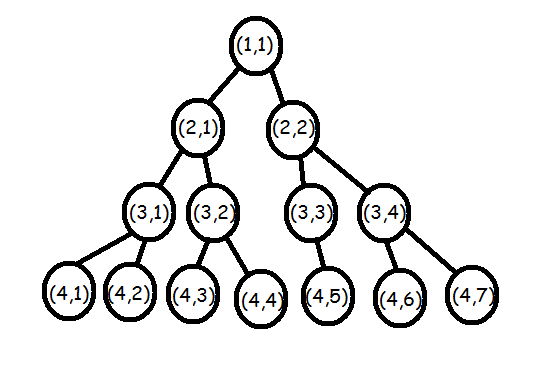
After the pseudo code is run, cell cnt[level] contains the number of vertices on level level. Cell left[level][position] contains the number of the vertex on the level level + 1, which is the left child of the vertex with index (level, position), or it contains -1, if the vertex doesn't have a left child. Similarly, cell right[level][position] is responsible for the right child. You can see how the tree with n = 4 looks like in the notes.
Serja loves to make things complicated, so he first made a tree and then added an empty set A(level, position) for each vertex. Then Sereja executes m operations. Each operation is of one of the two following types:
- The format of the operation is "1 t l r x". For all vertices level, position (level = t; l ≤ position ≤ r) add value x to set A(level, position).
- The format of the operation is "2 t v". For vertex level, position (level = t, position = v), find the union of all sets of vertices that are in the subtree of vertex (level, position). Print the size of the union of these sets.
Help Sereja execute the operations. In this problem a set contains only distinct values like std::set in C++.
The first line contains integers n and m (1 ≤ n, m ≤ 7000).
Next m lines contain the descriptions of the operations. The operation of the first type is given by five integers: 1 t l r x (1 ≤ t ≤ n; 1 ≤ l ≤ r ≤ cnt[t]; 1 ≤ x ≤ 106). The operation of the second type is given by three integers: 2 t v (1 ≤ t ≤ n; 1 ≤ v ≤ cnt[t]).
For each operation of the second type, print the answer on a single line.
4 5
1 4 4 7 1
1 3 1 2 2
2 1 1
2 4 1
2 3 3
2
0
1
You can find the definitions that are used while working with root trees by this link: http://en.wikipedia.org/wiki/Tree_(graph_theory)
You can see an example of a constructed tree at n = 4 below.
| Name |
|---|




