| Codeforces Round 236 (Div. 2) |
|---|
| Finished |
Let's call an undirected graph of n vertices p-interesting, if the following conditions fulfill:
- the graph contains exactly 2n + p edges;
- the graph doesn't contain self-loops and multiple edges;
- for any integer k (1 ≤ k ≤ n), any subgraph consisting of k vertices contains at most 2k + p edges.
A subgraph of a graph is some set of the graph vertices and some set of the graph edges. At that, the set of edges must meet the condition: both ends of each edge from the set must belong to the chosen set of vertices.
Your task is to find a p-interesting graph consisting of n vertices.
The first line contains a single integer t (1 ≤ t ≤ 5) — the number of tests in the input. Next t lines each contains two space-separated integers: n, p (5 ≤ n ≤ 24; p ≥ 0; 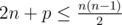 ) — the number of vertices in the graph and the interest value for the appropriate test.
) — the number of vertices in the graph and the interest value for the appropriate test.
It is guaranteed that the required graph exists.
For each of the t tests print 2n + p lines containing the description of the edges of a p-interesting graph: the i-th line must contain two space-separated integers ai, bi (1 ≤ ai, bi ≤ n; ai ≠ bi) — two vertices, connected by an edge in the resulting graph. Consider the graph vertices numbered with integers from 1 to n.
Print the answers to the tests in the order the tests occur in the input. If there are multiple solutions, you can print any of them.
1
6 0
1 2
1 3
1 4
1 5
1 6
2 3
2 4
2 5
2 6
3 4
3 5
3 6
| Name |
|---|




