| Codeforces Round 254 (Div. 1) |
|---|
| Finished |
DZY loves Physics, and he enjoys calculating density.
Almost everything has density, even a graph. We define the density of a non-directed graph (nodes and edges of the graph have some values) as follows:
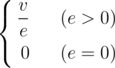
Once DZY got a graph G, now he wants to find a connected induced subgraph G' of the graph, such that the density of G' is as large as possible.
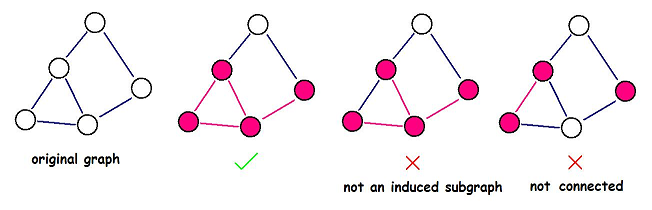
An induced subgraph G'(V', E') of a graph G(V, E) is a graph that satisfies:
-
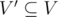 ;
; - edge
 if and only if
if and only if 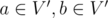 , and edge
, and edge 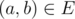 ;
; - the value of an edge in G' is the same as the value of the corresponding edge in G, so as the value of a node.
Help DZY to find the induced subgraph with maximum density. Note that the induced subgraph you choose must be connected.
The first line contains two space-separated integers n (1 ≤ n ≤ 500),  . Integer n represents the number of nodes of the graph G, m represents the number of edges.
. Integer n represents the number of nodes of the graph G, m represents the number of edges.
The second line contains n space-separated integers xi (1 ≤ xi ≤ 106), where xi represents the value of the i-th node. Consider the graph nodes are numbered from 1 to n.
Each of the next m lines contains three space-separated integers ai, bi, ci (1 ≤ ai < bi ≤ n; 1 ≤ ci ≤ 103), denoting an edge between node ai and bi with value ci. The graph won't contain multiple edges.
Output a real number denoting the answer, with an absolute or relative error of at most 10 - 9.
1 0
1
0.000000000000000
2 1
1 2
1 2 1
3.000000000000000
5 6
13 56 73 98 17
1 2 56
1 3 29
1 4 42
2 3 95
2 4 88
3 4 63
2.965517241379311
In the first sample, you can only choose an empty subgraph, or the subgraph containing only node 1.
In the second sample, choosing the whole graph is optimal.
| Name |
|---|




