| Bayan 2015 Contest Warm Up |
|---|
| Finished |
Consider infinite grid of unit cells. Some of those cells are planets.
Meta-universe M = {p1, p2, ..., pk} is a set of planets. Suppose there is an infinite row or column with following two properties: 1) it doesn't contain any planet pi of meta-universe M on it; 2) there are planets of M located on both sides from this row or column. In this case we can turn the meta-universe M into two non-empty meta-universes M1 and M2 containing planets that are located on respective sides of this row or column.
A meta-universe which can't be split using operation above is called a universe. We perform such operations until all meta-universes turn to universes.
Given positions of the planets in the original meta-universe, find the number of universes that are result of described process. It can be proved that each universe is uniquely identified not depending from order of splitting.
The first line of input contains an integer n, (1 ≤ n ≤ 105), denoting the number of planets in the meta-universe.
The next n lines each contain integers xi and yi, ( - 109 ≤ xi, yi ≤ 109), denoting the coordinates of the i-th planet. All planets are located in different cells.
Print the number of resulting universes.
5
0 0
0 2
2 0
2 1
2 2
3
8
0 0
1 0
0 2
0 3
3 0
3 1
2 3
3 3
1
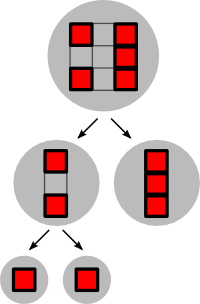
The following figure describes the first test case:
| Name |
|---|




