| Codeforces Round 278 (Div. 2) |
|---|
| Finished |
There is an old tradition of keeping 4 boxes of candies in the house in Cyberland. The numbers of candies are special if their arithmetic mean, their median and their range are all equal. By definition, for a set {x1, x2, x3, x4} (x1 ≤ x2 ≤ x3 ≤ x4) arithmetic mean is 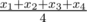 , median is
, median is 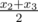 and range is x4 - x1. The arithmetic mean and median are not necessary integer. It is well-known that if those three numbers are same, boxes will create a "debugging field" and codes in the field will have no bugs.
and range is x4 - x1. The arithmetic mean and median are not necessary integer. It is well-known that if those three numbers are same, boxes will create a "debugging field" and codes in the field will have no bugs.
For example, 1, 1, 3, 3 is the example of 4 numbers meeting the condition because their mean, median and range are all equal to 2.
Jeff has 4 special boxes of candies. However, something bad has happened! Some of the boxes could have been lost and now there are only n (0 ≤ n ≤ 4) boxes remaining. The i-th remaining box contains ai candies.
Now Jeff wants to know: is there a possible way to find the number of candies of the 4 - n missing boxes, meeting the condition above (the mean, median and range are equal)?
The first line of input contains an only integer n (0 ≤ n ≤ 4).
The next n lines contain integers ai, denoting the number of candies in the i-th box (1 ≤ ai ≤ 500).
In the first output line, print "YES" if a solution exists, or print "NO" if there is no solution.
If a solution exists, you should output 4 - n more lines, each line containing an integer b, denoting the number of candies in a missing box.
All your numbers b must satisfy inequality 1 ≤ b ≤ 106. It is guaranteed that if there exists a positive integer solution, you can always find such b's meeting the condition. If there are multiple answers, you are allowed to print any of them.
Given numbers ai may follow in any order in the input, not necessary in non-decreasing.
ai may have stood at any positions in the original set, not necessary on lowest n first positions.
2
1
1
YES
3
3
3
1
1
1
NO
4
1
2
2
3
YES
For the first sample, the numbers of candies in 4 boxes can be 1, 1, 3, 3. The arithmetic mean, the median and the range of them are all 2.
For the second sample, it's impossible to find the missing number of candies.
In the third example no box has been lost and numbers satisfy the condition.
You may output b in any order.
| Name |
|---|




