| Codeforces Round 286 (Div. 2) |
|---|
| Finished |
Shuseki Kingdom is the world's leading nation for innovation and technology. There are n cities in the kingdom, numbered from 1 to n.
Thanks to Mr. Kitayuta's research, it has finally become possible to construct teleportation pipes between two cities. A teleportation pipe will connect two cities unidirectionally, that is, a teleportation pipe from city x to city y cannot be used to travel from city y to city x. The transportation within each city is extremely developed, therefore if a pipe from city x to city y and a pipe from city y to city z are both constructed, people will be able to travel from city x to city z instantly.
Mr. Kitayuta is also involved in national politics. He considers that the transportation between the m pairs of city (ai, bi) (1 ≤ i ≤ m) is important. He is planning to construct teleportation pipes so that for each important pair (ai, bi), it will be possible to travel from city ai to city bi by using one or more teleportation pipes (but not necessarily from city bi to city ai). Find the minimum number of teleportation pipes that need to be constructed. So far, no teleportation pipe has been constructed, and there is no other effective transportation between cities.
The first line contains two space-separated integers n and m (2 ≤ n ≤ 105, 1 ≤ m ≤ 105), denoting the number of the cities in Shuseki Kingdom and the number of the important pairs, respectively.
The following m lines describe the important pairs. The i-th of them (1 ≤ i ≤ m) contains two space-separated integers ai and bi (1 ≤ ai, bi ≤ n, ai ≠ bi), denoting that it must be possible to travel from city ai to city bi by using one or more teleportation pipes (but not necessarily from city bi to city ai). It is guaranteed that all pairs (ai, bi) are distinct.
Print the minimum required number of teleportation pipes to fulfill Mr. Kitayuta's purpose.
4 5
1 2
1 3
1 4
2 3
2 4
3
4 6
1 2
1 4
2 3
2 4
3 2
3 4
4
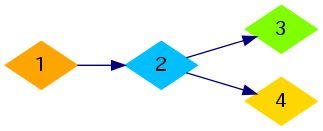
For the first sample, one of the optimal ways to construct pipes is shown in the image below:
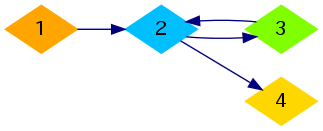
For the second sample, one of the optimal ways is shown below:
| Name |
|---|




