| Codeforces Round 309 (Div. 1) |
|---|
| Закончено |
Кёя Оотори хочет добраться до школы, воспользовавшись железнодорожным транспортом. Дано n станций и m односторонних железнодорожных маршрутов, соединяющих разные станции. Кёя находится на станции номер 1, а его школа — на станции n. Чтобы воспользоваться маршрутом, требуется заплатить за билет, после чего поезд едет определенное количество времени. Однако поезда несовершенны и доезжают до пункта назначения за некоторое случайное время. Если Кёя прибывает в школу строго более, чем через t единиц времени, ему придётся заплатить штраф в размере x.
Каждый маршрут описывается ценой за билет и распределением вероятностей для времени пути поезда. Более формально, для пути i известна стоимость билета ci, и распределение вероятностей pi, k, обозначающее вероятность того, что поезду, едущему по этому маршруту, потребуется k единиц времени для всех 1 ≤ k ≤ t. Времена путешествия всех поездов, используемых Кёей, являются совокупно независимыми случайными величинами (более того, если Кёя путешествует тем же самым поездом более одного раза, возможно, что поезд будет ехать разное время, и эти значения также независимы друг от друга).
Кёя хочет добраться до школы таким образом, чтобы минимизировать математическое ожидание количества потраченных им денег (за цены всех билетов плюс, возможно, штраф за опоздание). Кёя может модифицировать свой план по ходу поездки, основываясь на том, сколько времени у него остаётся. Каково матожидание количества денег, потраченных Кёей на пути в школу, если он будет действовать оптимально?
В первой строке ввода находятся четыре целых числа n, m, t, x (2 ≤ n ≤ 50, 1 ≤ m ≤ 100, 1 ≤ t ≤ 20 000, 0 ≤ x ≤ 106).
Следующие 2m строк содержат описания маршрутов.
В 2i-й строке находятся 3 целых числа ai, bi, ci, обозначающих односторонний маршрут от платформы ai до платформы bi, со стоимость билета ci (1 ≤ ai, bi ≤ n, ai ≠ bi, 0 ≤ ci ≤ 106). От каждой платформы существует как минимум один путь до школы.
В (2i + 1)-й строке находятся t целых чисел, pi, 1, pi, 2, ..., pi, t, где pi, k / 100000 — это вероятность того, что этому поезду потребуется k единиц времени на преодоление пути (0 ≤ pi, k ≤ 100 000 для 1 ≤ k ≤ t, 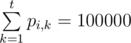 ).
).
Гарантируется, что между каждой парой платформ существует не более одного маршрута в каждом из направлений.
Выведите единственное действительное число, равное математическому ожиданию стоимости дороги в школу. Ответ будет засчитан, если его относительная или абсолютная погрешность относительно авторского ответа не превышает 10 - 6.
4 4 5 1
1 2 0
50000 0 50000 0 0
2 3 0
10000 0 0 0 90000
3 4 0
100000 0 0 0 0
2 4 0
0 0 0 50000 50000
0.7000000000
4 4 5 1
1 2 100
50000 0 50000 0 0
2 3 100
10000 0 0 0 90000
3 4 100
100000 0 0 0 0
2 4 100
0 0 0 50000 50000
200.7500000000
Оптимальная стратегия в первом тесте из условия такова:
Сперва надо проехать по первому маршруту. С вероятностью 1 / 2 у Кёи это займёт 1 единицу времени. В противном случае, Кёя потратит 3 единиц времени.
Если поезд пройдет маршрут за 1 единицы времени, надо проехать по четвёртому маршруту. Кёя доберется до школы вовремя с вероятностью 1 / 2. В противном случае, если поезд едет за 3 единицы времени, надо проехать по второму маршруту. Кёя доберется до школы вовремя с вероятностью 1 / 10.
Так как стоимость всех путей равняется нулю, достаточно определить вероятность того, что Кёя получит штраф за опоздание. Вероятность того, что Кёя будет должен заплатить штраф, равна 1 / 2 × 1 / 2 + 1 / 2 × 9 / 10 = 7 / 10. Можно показать, что никакая другая стратегия не даёт меньшего математического ожидания штрафа.
Оптимальная стратегия во втором тесте из условия — проехать по маршруту 1 → 2 → 4, что бы ни произошло. Кёя получит штраф с вероятностью 3 / 4, а суммарная стоимость билетов равна 200, следовательно, ожидаемая стоимость всей поездки — 200.75.
| Название |
|---|




