| Codeforces Round 316 (Div. 2) |
|---|
| Finished |
One day Misha and Andrew were playing a very simple game. First, each player chooses an integer in the range from 1 to n. Let's assume that Misha chose number m, and Andrew chose number a.
Then, by using a random generator they choose a random integer c in the range between 1 and n (any integer from 1 to n is chosen with the same probability), after which the winner is the player, whose number was closer to c. The boys agreed that if m and a are located on the same distance from c, Misha wins.
Andrew wants to win very much, so he asks you to help him. You know the number selected by Misha, and number n. You need to determine which value of a Andrew must choose, so that the probability of his victory is the highest possible.
More formally, you need to find such integer a (1 ≤ a ≤ n), that the probability that 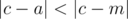 is maximal, where c is the equiprobably chosen integer from 1 to n (inclusive).
is maximal, where c is the equiprobably chosen integer from 1 to n (inclusive).
The first line contains two integers n and m (1 ≤ m ≤ n ≤ 109) — the range of numbers in the game, and the number selected by Misha respectively.
Print a single number — such value a, that probability that Andrew wins is the highest. If there are multiple such values, print the minimum of them.
3 1
2
4 3
2
In the first sample test: Andrew wins if c is equal to 2 or 3. The probability that Andrew wins is 2 / 3. If Andrew chooses a = 3, the probability of winning will be 1 / 3. If a = 1, the probability of winning is 0.
In the second sample test: Andrew wins if c is equal to 1 and 2. The probability that Andrew wins is 1 / 2. For other choices of a the probability of winning is less.
| Name |
|---|




