| Codeforces Round 319 (Div. 1) |
|---|
| Finished |
On a plane are n points (xi, yi) with integer coordinates between 0 and 106. The distance between the two points with numbers a and b is said to be the following value: 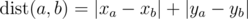 (the distance calculated by such formula is called Manhattan distance).
(the distance calculated by such formula is called Manhattan distance).
We call a hamiltonian path to be some permutation pi of numbers from 1 to n. We say that the length of this path is value 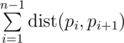 .
.
Find some hamiltonian path with a length of no more than 25 × 108. Note that you do not have to minimize the path length.
The first line contains integer n (1 ≤ n ≤ 106).
The i + 1-th line contains the coordinates of the i-th point: xi and yi (0 ≤ xi, yi ≤ 106).
It is guaranteed that no two points coincide.
Print the permutation of numbers pi from 1 to n — the sought Hamiltonian path. The permutation must meet the inequality 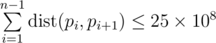 .
.
If there are multiple possible answers, print any of them.
It is guaranteed that the answer exists.
5
0 7
8 10
3 4
5 0
9 12
4 3 1 2 5
In the sample test the total distance is:

(|5 - 3| + |0 - 4|) + (|3 - 0| + |4 - 7|) + (|0 - 8| + |7 - 10|) + (|8 - 9| + |10 - 12|) = 2 + 4 + 3 + 3 + 8 + 3 + 1 + 2 = 26
| Name |
|---|




