| Codeforces Round 330 (Div. 1) |
|---|
| Finished |
Edo has got a collection of n refrigerator magnets!
He decided to buy a refrigerator and hang the magnets on the door. The shop can make the refrigerator with any size of the door that meets the following restrictions: the refrigerator door must be rectangle, and both the length and the width of the door must be positive integers.
Edo figured out how he wants to place the magnets on the refrigerator. He introduced a system of coordinates on the plane, where each magnet is represented as a rectangle with sides parallel to the coordinate axes.
Now he wants to remove no more than k magnets (he may choose to keep all of them) and attach all remaining magnets to the refrigerator door, and the area of the door should be as small as possible. A magnet is considered to be attached to the refrigerator door if its center lies on the door or on its boundary. The relative positions of all the remaining magnets must correspond to the plan.
Let us explain the last two sentences. Let's suppose we want to hang two magnets on the refrigerator. If the magnet in the plan has coordinates of the lower left corner (x1, y1) and the upper right corner (x2, y2), then its center is located at (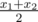 ,
, 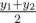 ) (may not be integers). By saying the relative position should correspond to the plan we mean that the only available operation is translation, i.e. the vector connecting the centers of two magnets in the original plan, must be equal to the vector connecting the centers of these two magnets on the refrigerator.
) (may not be integers). By saying the relative position should correspond to the plan we mean that the only available operation is translation, i.e. the vector connecting the centers of two magnets in the original plan, must be equal to the vector connecting the centers of these two magnets on the refrigerator.
The sides of the refrigerator door must also be parallel to coordinate axes.
The first line contains two integers n and k (1 ≤ n ≤ 100 000, 0 ≤ k ≤ min(10, n - 1)) — the number of magnets that Edo has and the maximum number of magnets Edo may not place on the refrigerator.
Next n lines describe the initial plan of placing magnets. Each line contains four integers x1, y1, x2, y2 (1 ≤ x1 < x2 ≤ 109, 1 ≤ y1 < y2 ≤ 109) — the coordinates of the lower left and upper right corners of the current magnet. The magnets can partially overlap or even fully coincide.
Print a single integer — the minimum area of the door of refrigerator, which can be used to place at least n - k magnets, preserving the relative positions.
3 1
1 1 2 2
2 2 3 3
3 3 4 4
1
4 1
1 1 2 2
1 9 2 10
9 9 10 10
9 1 10 2
64
3 0
1 1 2 2
1 1 1000000000 1000000000
1 3 8 12
249999999000000001
In the first test sample it is optimal to remove either the first or the third magnet. If we remove the first magnet, the centers of two others will lie at points (2.5, 2.5) and (3.5, 3.5). Thus, it is enough to buy a fridge with door width 1 and door height 1, the area of the door also equals one, correspondingly.
In the second test sample it doesn't matter which magnet to remove, the answer will not change — we need a fridge with door width 8 and door height 8.
In the third sample you cannot remove anything as k = 0.
| Name |
|---|




