| Codeforces Round 340 (Div. 2) |
|---|
| Finished |
A flowerbed has many flowers and two fountains.
You can adjust the water pressure and set any values r1(r1 ≥ 0) and r2(r2 ≥ 0), giving the distances at which the water is spread from the first and second fountain respectively. You have to set such r1 and r2 that all the flowers are watered, that is, for each flower, the distance between the flower and the first fountain doesn't exceed r1, or the distance to the second fountain doesn't exceed r2. It's OK if some flowers are watered by both fountains.
You need to decrease the amount of water you need, that is set such r1 and r2 that all the flowers are watered and the r12 + r22 is minimum possible. Find this minimum value.
The first line of the input contains integers n, x1, y1, x2, y2 (1 ≤ n ≤ 2000, - 107 ≤ x1, y1, x2, y2 ≤ 107) — the number of flowers, the coordinates of the first and the second fountain.
Next follow n lines. The i-th of these lines contains integers xi and yi ( - 107 ≤ xi, yi ≤ 107) — the coordinates of the i-th flower.
It is guaranteed that all n + 2 points in the input are distinct.
Print the minimum possible value r12 + r22. Note, that in this problem optimal answer is always integer.
2 -1 0 5 3
0 2
5 2
6
4 0 0 5 0
9 4
8 3
-1 0
1 4
33
The first sample is (r12 = 5, r22 = 1):  The second sample is (r12 = 1, r22 = 32):
The second sample is (r12 = 1, r22 = 32): 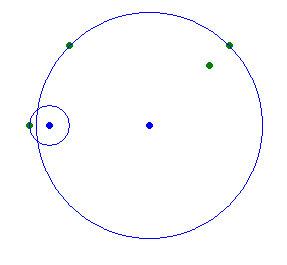
| Name |
|---|




